动态规划
动态规划(Dynamic Programming)基本思想
动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的过程。动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式 。
看一个例子,比如求斐波那契(Fibonacci)数列的第N项
斐波那契数列:1 1 2 3 5 8 13 21.....
fib(1) = 1
fib(2) = 1
fib(3) = 2
fib(n) = fib(n-1) + fib(n-2)
那一般我们都会使用到递归的方法来求第N项的值
#include <iostream>
using namespace std;
int fib(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
else
return fib(n - 1) + fib(n - 2);
}
int main()
{
int n;
cin >> n;
cout << fib(n) << endl;
return 0;
}
时间复杂度为2^n
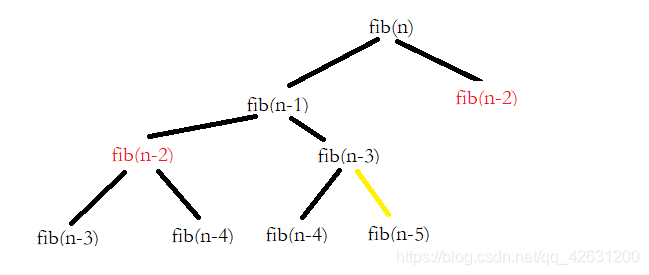
使用递归算法那就是如下图这样的计算方式。我们可以发现这种计算方式存在许多重叠子问题,如fib(n-2)、fib(n-3)等都重复计算了,这样就产生生了不必要的计算,所以使用动态规划思想的的话,我们可以定义一个F[ ]向量,将fib(n-2)、fib(n-3)等的结果存到其中,这样做的最终结果就是我们只需要计算左边部分。时间复杂度也因此降为O(n)。
从递归到动态规划
1、自上而下(备忘录法)
时间复杂度、空间复杂度皆为O(n)。
#include <iostream>
#include <vector>
using namespace std;
int fib(int n)
{
vector<int> F(n + 1, 0);
if (n == 1 || n == 2)
return 1;
if (F[n] != 0)
return F[n];
else
{
F[n] = fib(n - 1) + fib(n - 2);
}
return F[n];
}
int main()
{
int n;
cin >> n;
cout << fib(n) << endl;
return 0;
}2、自下而上(回溯法)
从最后一步的递归(fib(0))开始反推结果。
时间复杂度O(n)、空间复杂度O(1)。
#include <iostream>
using namespace std;
int fib(int n)
{
if (n <= 1)
return n;
int F[10000];
F[1] = 1;
F[2] = 1;
for (int i = 3; i <= n; i++)
{
F[i] = F[i - 1] + F[i - 2];
}
return F[n];
}
int main()
{
int n;
cin >> n;
cout << fib(n) << endl;
return 0;
}从第N向的表达式来看,我们只需要维护两个数就可以了,不需要记录整个序列。
int fib(int n)
{
if (n <= 1)
return n;
int F[2];
F[0] = 1;
F[1] = 1;
for (int i = 3; i <= n; i++)
{
int temp = F[0] + F[1];
F[0] = F[1];
F[1] = temp;
}
return F[1];
}时间复杂度O(n),空间复杂度O(1).