当前位置：首页 > news >正文

有向图的强连通分量

news 来源：原创 2024/4/26 2:23:46

文章目录

一些定义
求强连通分量
检查点是否在scc中
tarjam求scc
缩点
- 拓扑序深搜做法
例题
- 受欢迎的牛
- - 题意
  - 做法
  - 代码
- 学校网络
- - 思路
  - debug
  - 代码
- 最大半连通子图
- - 题意
  - 思想
  - 代码
- 银河
- - 代码

一些定义

在这里插入图片描述
强连通分量：又叫极大连通分量，对于一个连通分量，如果在加上任何一个点之后，都不是连通分量了，就叫强连通分量

强连通分量作用：将任意一个有向图，通过缩点，转化成有向无环图（DAG），也就是拓扑图

缩点指的是将所有的连通分量缩成一个点

例如：
在这里插入图片描述
图中圈出来的部分就是一个强连通分量，缩点就是把中间的连通分量当成一个点，然后其他的单独的点也是一个连通分量，也就是上图缩完之后就只有五个点了

也就是这样一个有向无环图，好处就是在求最短路或者最长路的时候，可以按照拓扑序从前往后直接递推一遍就可以了，时间复杂度是O（n + m）的

求强连通分量

按照DFS的顺序来求

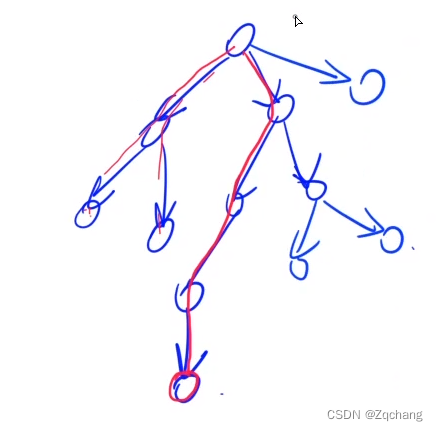
在这里插入图片描述
把所有的边分为四大类

第一类：树枝边：(x, y)要求x是y的父节点
第二类：前向边：(x, y)要求x是y的祖先节点，树枝边是一种特殊的前向边，也就是下图这样
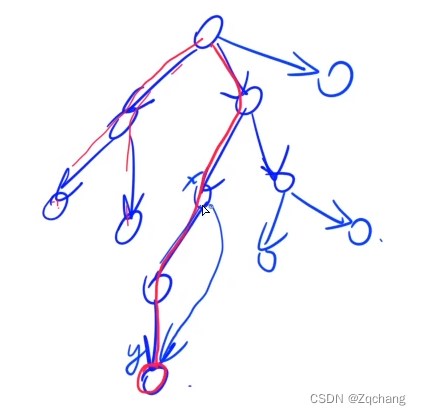
在这里插入图片描述

第三类：后向边：(x, y)，将上图中的x ->y的边方向反过来就可以
第四类：横叉边：(x, y)，往我搜过的其他分支搜的时候，连向其他分支的一条边，被称为横叉边图中从x点指向最左边的那个点的边就是横叉边，但是右边那个不是，那个是树枝边
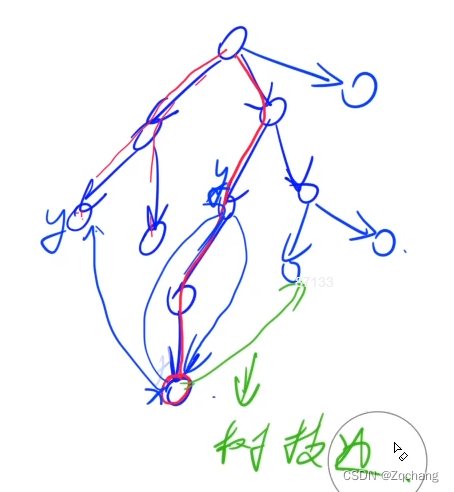
在这里插入图片描述
强连通分量简称scc

检查点是否在scc中

如果一个点在scc中，那么一定是它沿着后向边，走到了当前这个正在搜索的路径上，当前红色的就是递归的路径
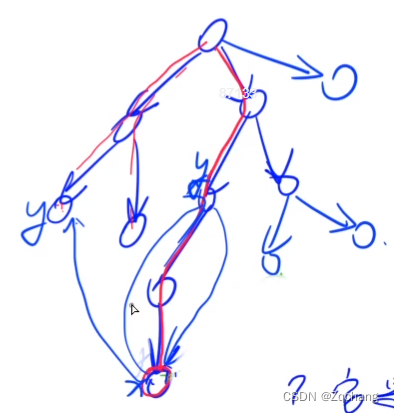
在这里插入图片描述
情况1:存在后向边指向祖先节点
情况2：先走到横叉边，横叉边再往上走到祖先节点
对于任意的前向边，都不会构成回路，不需要管
所以存在scc一定是上面两种情况，当然，可能有自环

tarjam求scc

时间戳：搜索的时候，按照dfs的顺序给每个点一个编号
在这里插入图片描述
求强连通分量的时候，是求scc最上面的一个点，模板如下，求强连通分量，时间复杂度是线性的，每个点只会遍历一次，也就是O(n + m)

void tarjan(int u)
{
    dfn[u] = low[u] = ++ timestamp;//时间戳
    stk[ ++ top] = u, in_stk[u] = true;//加入栈中，这个栈里面存的是还没有遍历完的强连通分量
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        }
        else if (in_stk[j]) low[u] = min(low[u], dfn[j]);
    }

    if (dfn[u] == low[u])
    {
        ++ scc_cnt;
        int y;
        do {
            y = stk[top -- ];
            in_stk[y] = false;
            id[y] = scc_cnt;
            Size[scc_cnt] ++ ;
        } while (y != u);
    }
}

缩点

遍历一下所有边
在这里插入图片描述
注意，如果i和j是同一个连通分量中的话不要加边，加上的话，就相当于加上自环了，不是DAG了

注意！scc缩点之后，按照编号就已经是拓扑序了，不需要额外跑拓扑序

拓扑序深搜做法

拓扑序除了宽搜之外，还能用深搜来做
先传入一个u，然后遍历u的邻边，之后把u加入到序列之中，最后得到的序列一定是拓扑的逆序

例题

受欢迎的牛

题意

给你一个图，让你看看有多少个点是其他点都能走到的

做法

只需要在反图上出发遍历所有的点，判断一下这个点是否能遍历到所有点就可以

但是，如果这个图是拓扑图的话，这个题就简单起来了，则只需要看是不是只有一个出度为0，如果存在超过两个，则说明至少有一个不被另一个喜欢，答案就是0

所以这个题缩点之后，变成DAG，就看出度为0的点有几个，如果只有一个的话，答案就是这个缩点的强连通分量中点的数量

对于这个题，不需要真的把图建出来，只需要遍历一下所有的边，统计一下点的出度就可以

代码

#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
#define endl '\n'
#define int long long
#define fast ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
const int N = 10010, M = 50010;
int n, m;
vector<int> v[N];
int dfn[N], low[N], ts;
int stk[N], top;
bool vis[N], in_stk[N]; 
int id[N], scc_cnt, sz[N];
int out[N];

void tarjan(int u)
{
    dfn[u] = low[u] = ++ ts;
    stk[++ top] = u, vis[u] = 1;
    for(auto i : v[u])
    {
        if(!dfn[i])
        {
            tarjan(i);
            low[u] = min(low[u], low[i]);
        }
        else if(vis[i]) low[u] = min(low[u], dfn[i]);
    }
    
    if(dfn[u] == low[u])
    {
        ++ scc_cnt;
        int y;
        do
        {
            y = stk[top --];
            vis[y] = 0;
            id[y] = scc_cnt;
            sz[scc_cnt] ++;
        }while(y != u);
    }
}

signed main()
{ 
    fast;
    cin >> n >> m;
    while (m -- )
    {
        int a, b;
        cin >> a >> b;
        v[a].push_back(b);
    }
    
    for(int i=1; i<=n; i++) if(!dfn[i]) tarjan(i);
    
    for (int i = 1; i <= n; i ++ )
    {
        for(auto j : v[i])
        {
            int a = id[i], b = id[j];//a表示i点所在连通分量，b表示j
            if(a != b) out[a] ++; //如果不在一个里面
        }
    }
    
    int zero = 0, sum = 0;
    for (int i = 1; i <= scc_cnt; i ++ ) 
        if(!out[i])
        {
            zero ++;
            sum += sz[i];
            if(zero > 1) 
            {
                sum = 0;
                break;
            }
        }
    
    cout << sum << endl;
    return 0;
}

学校网络

学校网络
就是我们需要把一个图变成强连通分量，最少需要加多少条边

思路

如果通过缩点把它变成一个有向无环图的话，是不是会变得比较简单呢？
缩完之后，假设一开始有p个入度为0的点，也就是p个起点，还有q个终点（出度为0），因此至少给p个点发信息，也就是第一问答案就是p，第二问结论是最少加max(p, q)；证明自己去看视频

然后就，，就跟板子一样

debug

Y总传送debug小技巧，就是二分debug，从一半开始输出，慢慢缩小范围

代码

#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
#define endl '\n'
#define int long long
#define fast ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
const int N = 110;
int n, m;
vector<int> v[N];
int dfn[N], low[N], ts;
int stk[N], top;
bool vis[N], in_stk[N]; 
int id[N], scc_cnt, sz[N];
int out[N], in[N];

void tarjan(int u)
{
    dfn[u] = low[u] = ++ ts;
    stk[++ top] = u, vis[u] = 1;
    for(auto i : v[u])
    {
        if(!dfn[i])
        {
            tarjan(i);
            low[u] = min(low[u], low[i]);
        }
        else if(vis[i]) low[u] = min(low[u], dfn[i]);
    }
    
    if(dfn[u] == low[u])
    {
        ++ scc_cnt;
        int y;
        do
        {
            y = stk[top --];
            vis[y] = 0;
            id[y] = scc_cnt;
            sz[scc_cnt] ++;
        }while(y != u);
    }
}

signed main()
{ 
    fast;
    cin >> n;
    for(int i=1; i<=n; i++)
    {
        int t;
        while (cin >> t, t) v[i].push_back(t);
        
    }
    
    for(int i=1; i<=n; i++) if(!dfn[i]) tarjan(i);
    
    for (int i = 1; i <= n; i ++ )
    {
        for(auto j : v[i])
        {
            int a = id[i], b = id[j];//a表示i点所在连通分量，b表示j
            if(a != b) //如果不在一个里面
            {
                out[a] ++; 
                in[b] ++;
            }
        }
    }
    
    int a = 0, b = 0;
    for (int i = 1; i <= scc_cnt; i ++ )
    {
        if (!in[i]) a ++ ;
        if (!out[i]) b ++ ;
    }

    cout << a << endl;
    if (scc_cnt == 1) cout << 0 << endl;
    else cout << max(a, b) << endl;

    return 0;
}

最大半连通子图

题意

就是求最大半连通子图

思想

在一个强连通分量当中，如果我们选择了强连通分量中的一部分点，还不如全部选上，因为这里面所有的点，都是可以相互到达的，强连通必然是半连通，所以缩点，得到DAG之后，就选一个链，这个一定满足要求，注意，这个链是不能分叉的，分叉之后不一定能满足可以到达的条件，因此，这个题就是要找一个最长的链。

可以用递推的方式来做，f[i]表示以第i个点为终点的最长链的节点数量之和是多少，也就是跑一个最长路，拓扑图上的最长路问题就是dp问题，就看一下所有i这个点的前驱，从前驱里面取一个最大值f[i]就可以，同时搞一个g[i]表示让f[i]取得最大值的方案数，这里就是一个很经典的统计最大值方案的问题，方程可以推出
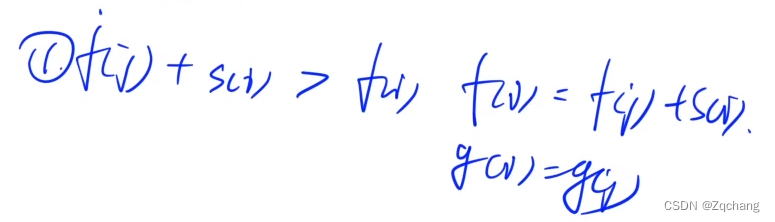
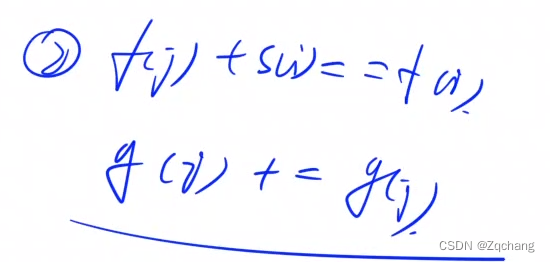
在这里插入图片描述

注意：这里方案数的不同指的是最少有一个点是不同的，如果有一条边是不同的不算是不同的导出子图（根据定义可以得知，一个点如果被选中的话，与之相关的所有边都会被选中）

所以建图过程中对边直接去重就行，而且，我们计算方案数的时候是根据边来判的，因此，必须去重

总三步
1.tarjan
2.缩点建图，给重边去重
3.按照拓扑序递推

代码

#include<bits/stdc++.h>
using namespace std;
#define fast ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define x first
#define y second
#define PII pair<int, int>
#define ll long long
const int N = 100010;

int n, m, mod;
int id[N], scc_cnt, top, dfn[N], stk[N], ts, low[N], in_stk[N], vis[N];
int sz[N], f[N], g[N];
vector<int> v[N], vv[N];

void tarjan(int u)
{
    dfn[u] = low[u] = ++ ts;
    stk[++ top] = u, in_stk[u] = 1;
    for(auto i: v[u])
    {
        if(!dfn[i])
        {
            tarjan(i);
            low[u] = min(low[u], low[i]);
        }
        else if(in_stk[i]) low[u] = min(low[u], dfn[i]);
    }
    
    if(dfn[u] == low[u])
    {
        ++ scc_cnt;
        int y;
        do{
            y = stk[top --];
            in_stk[y] = 0;
            id[y] = scc_cnt;
            sz[scc_cnt] ++;
        }while(y != u);
    }
}

signed main()
{
    fast;
    cin >> n >> m >> mod;
    int a, b;
    while (m -- )
    {
        cin >> a >> b;
        v[a].push_back(b);
    }
    
    for (int i = 1; i <= n; i ++ ) if(!dfn[i]) tarjan(i);
    
    unordered_set<ll> s;
    
    for (int i = 1; i <= n; i ++ )
    {
        for(auto j : v[i])
        {
            a = id[i], b = id[j];
            int c = a * 1000000ll + b;
            if(a != b && !s.count(c))
            {
                vv[a].push_back(b);
                s.insert(c);
            }
        }
    }
    
    for(int i=scc_cnt; i>=1; i--)
    {
        if(!f[i])
        {
            f[i] = sz[i];
            g[i] = 1;
        }
        for(auto j  : vv[i])
        {
            if(f[j] < f[i] + sz[j])
            {
                f[j] = f[i] + sz[j];
                g[j] = g[i];
            }
            else if(f[j] == f[i] + sz[j]) g[j] = (g[j] + g[i]) % mod;
        }
    }
    
    int maxf = 0, sum = 0;
    
    for(int i=1; i<=scc_cnt; i ++)
        if(f[i] > maxf)
        {
            maxf = f[i];
            sum = g[i];
        }
        else if (f[i] == maxf) sum = (sum + g[i]) % mod;

    
    cout << maxf << endl;
    cout << sum << endl;
    return 0;
}