量子计算（八）：观测量和计算基下的测量
文章目录
观测量和计算基下的测量
一、观测量
二、计算基下的测量
三、投影测量
观测量和计算基下的测量
一、观测量
量子比特（qubit）不同于经典的比特（bit），一个量子比特|>可以同时处于|0>和|1>两个状态，可用线性代数中的线性组合（linear combination）来表示为
在量子力学中常称量子比特|>处于|0>和|1>的叠加态（superpositions），其中
、
都是复数（complex number），两维复向量空间的一组标准正交基（orthonormal basis）|0>和|1>组成一组计算基（computational basis）。
量子比特的信息不能直接获取，而是通过测量来获取量子比特的可观测的信息。可观测量在量子理论中由自伴算子（self-adjoint operators）来表征，自伴的有时也称Hermitian。量子理论中的可观测量与经典力学中的动力学量，如位置、动量和角动量等对应，而系统的其他特征，如质量或电荷，并不在可观测量的类别之中，它是作为参数被引入到系统的哈密顿量（Hamiltonian）。
在量子力学中测量（measure）会导坍塌，即是说测量会影响到原来的量子状态，因此量子状态的全部信息不可能通过一次测量得到。当对量子比特进行测量时，仅能得到该量子比特概率处在|0>态，或概率
处在|1>态。由于所有情况的概率和为1，则有
。
当对量子进行测量时，会发生什么变化呢？
假设：量子测量是由测量算子(measurement operators）的集合来描述，这些算子可以作用在待测量系统的状态空间（state space）上。指标
表示在实验上可能发生的结果。如果测量前的量子系统处在最新状态|
>，那么结果
发生的概率为
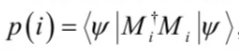
并且测量后的系统状态变为
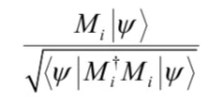
由于所有可能情况的概率和为1，即
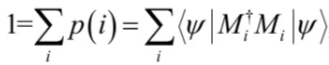
因此，测量算子需满足
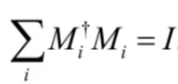
该方程被称为完备性方程(completeness equation）。
二、计算基下的测量
在计算基下单量子比特的测量，单量子比特在计算基下有两个测量算子分别是
。注意到这两个测量算子都是自伴的，即
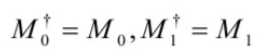
且
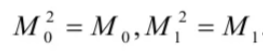
因此
该测量算子满足完备性方程。
设系统被测量时的状态是
，则测量结果为0的概率为
对应测量后的状态为
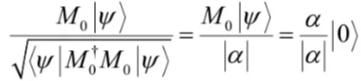
测量结果为1的概率为
测量后的状态为
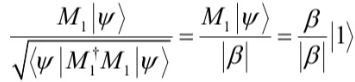
量子测量有很多种方式，比如投影测量（projective measurements）、POVM 测量(Positive Operator-Valued Measure）。
三、投影测量
为什么要介绍投影测量呢？因为当测量算子具有酉变换性质时，投影测量和一般测量等价。
投影测量由一个可观测量（observable）来描述，可观测量
是一个待观测系统的状态空间上的自伴算子。可观测量
可以写成谱分解的形式
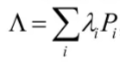
这里的为在
的特征值
对应特征空间上的投影。测量的可能结果对应于可观测量
的特征值
。在对状态|
>测量之后，得到结果
的概率为
若测量后，结果发生，则量子系统最新的状态为
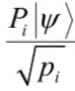
投影测量有一个重要的特征就是很容易计算投影测量的平均值。
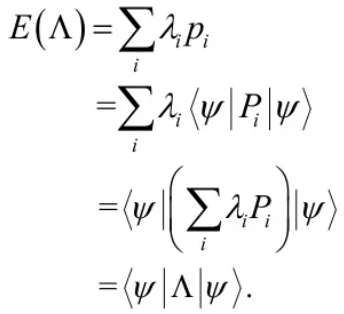
这个公式它能够简化很多计算。观测量的平均值通常也记作
。因此，观测量的标准差（standard deviation）
满足
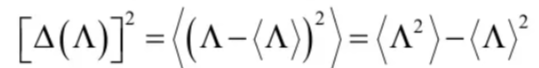
标准差是一个刻画典型分散程度的度量。
- 📢博客主页：https://lansonli.blog.csdn.net
- 📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正！
- 📢本文由 Lansonli 原创，首发于 CSDN博客🙉
- 📢停下休息的时候不要忘了别人还在奔跑，希望大家抓紧时间学习，全力奔赴更美好的生活✨