机器学习python实践——关于ward聚类分层算法的一些个人心得
最近在利用python跟着参考书进行机器学习相关实践,相关案例用到了ward算法,但是我理论部分用的是周志华老师的《西瓜书》,书上没有写关于ward的相关介绍,所以自己网上查了一堆资料,都很难说清楚ward算法,幸好最后在何晓群老师的《多元统计分析》这本书找到了比较清晰的说法,所以总结出了一些心得,在这篇文章中记录一下,同时,分享给广大网友,大家一起探讨一下,如果有误,也请谅解。当然,如果这篇文章还能入得了各位“看官”的法眼,麻烦点赞、关注、收藏,支持一下!
本文主要从三个方面进行说明:1、方差、离差平方和;2、ward算法原理;3、ward算法距离推导公式举例说明
一、方差、离差平方和
方差:
![]()
离差平方和:

对比方差和离差平方和公式,我们可以清楚的看到,离差平方和就是方差公式中的分子部分
另外,我对于离差平方和有两点我要解释一下:
第一点:可能很多人在网上看到的离差平方和公式跟我给出的有点区别,但是两者是一样的,只是网上大部分是拆开并且化简过得,而我这个是和起来的,同样因为我ward算法看的是何晓群老师的书,所以跟书上的表达方式保持一致
第二点:可能很多人在网上看到的离差平方和的符号是ESS,但是我这里却用SS表示,这个我觉得有必要跟大家说清楚,ESS表示的是回归平方和,SS才是离差平方和,两者是完全不同的东西,对此若有质疑,可以查看下面的链接,链接来源于百度百科:
离差平方和_百度百科 (baidu.com);回归平方和_百度百科 (baidu.com)
同时,对于方差,大家网上看到最多的形式应该是上述的形式,但是在聚类分析中,数据点常常是多维数据,所以很多人可能不太清楚对于多维数据方差该如何计算,下面举个二维数据的例子,大家看一下。每个样本通常由两个特征(例如坐标)组成,如(x1,x2),所以方差如下:
![]()
其中![]() 表示第i个样本点的第一个特征,
表示第i个样本点的第一个特征,![]() 表示样本均值点的第一个特征
表示样本均值点的第一个特征
从上述的公式,我们也就可以知道,离差平方和其实就等于每个样本点到样本均值点的距离的平方和
二、ward算法原理
ward算法认为同类样本之间的离差平方和应该尽量小,不同类之间的离差平方和应该尽量大。
假设,现在有n个样本,我们要将他分成k类,那么第t类样本的离差平和![]() 以及整个类内的离差平方和
以及整个类内的离差平方和![]() 如下所示:
如下所示:
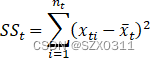
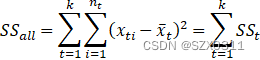
其中,![]() 表示第t类样本的个数,
表示第t类样本的个数,![]() 表示第t类样本中的第i个样本,
表示第t类样本中的第i个样本,![]() 表示第t类样本的均值点
表示第t类样本的均值点
ward算法的目标就是使得聚类完成之后整个类内的离差平方和![]() 达到极小,至于为什么,下面解释一下:
达到极小,至于为什么,下面解释一下:
从上面的公式中,我们可以看出来,整个类内的离差平方和![]() 就是对各类样本的离差平方和
就是对各类样本的离差平方和![]() 的求和,因为ward要求同类样本之间的离差平方和最小,即
的求和,因为ward要求同类样本之间的离差平方和最小,即![]() 要求最小,所以整个类内的离差平方和
要求最小,所以整个类内的离差平方和![]() 也会达到最小
也会达到最小
注意:整个类内的离差平方和不等于不同类之间的离差平方和
引用何晓群老师《多元统计分析》一书中的原话:如果直接将所有分类可能性的离差平方和算出来,然后找出使l![]() 达到极小的分类,那么这个计算量是巨大的,对计算机要求是非常高的,因此,ward算法是一种寻找局部最优解的方法,其思想就是先让n个样品各自成一类,然后每次缩小一类,每缩小一类,离差平方和就要增大,选择使
达到极小的分类,那么这个计算量是巨大的,对计算机要求是非常高的,因此,ward算法是一种寻找局部最优解的方法,其思想就是先让n个样品各自成一类,然后每次缩小一类,每缩小一类,离差平方和就要增大,选择使![]() 增加最小的两类合并,直到所有的样品归为一类为止
增加最小的两类合并,直到所有的样品归为一类为止
我们应该都知道层次聚类算法,本质上都是通过距离来对样本进行聚类操作,距离相近的簇(类)会被划分到同一簇中,所以,ward算法也为我们提供了一种簇间距的算法,帮助我们直接通过对簇间距的计算来近似获得局部最优解,公式如下:

np表示Gp类中样本个数,nk表示Gk类中的样本个数,nr表示Gr类中的样本个数
可能有些小伙伴对于这个上面的距离递推公式看的很迷,所以下面我会借用SciPy帮助文档例子进行举例说明
三、ward算法距离推导公式举例说明
SciPy帮助文档例子的代码如下:
from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt
X = [[i] for i in [2, 8, 0, 4, 1, 9, 9, 0]]
Z = linkage(X, 'ward')
fig = plt.figure(figsize=(25, 10))
dn = dendrogram(Z)
print(Z)
plt.show()通过代码我们知道输入的是数组X,输出的是链接数组Z,其中X是一个8行1列的二维数组,每一行数据都代表着一个位置标记,同时,根据网上大佬的说法Z是一个n行4列的数组,前两列表示要聚类的簇的编号,第三列表示两个即将聚类的簇之间的距离,第四列表示聚类所得的新簇中含有的样本个数
Z的输出如下:
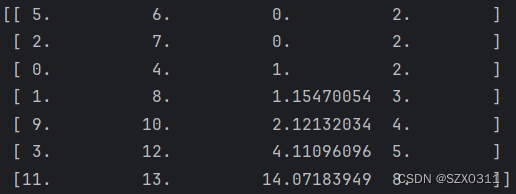
对应于第一行数据可能有些小伙伴会觉得疑惑,5、6是哪里来的?因为上文中已经说过了ward算法会先n个样本各成一类,所以5、6代表数组X的8个样本中编号为5和6的样本,数组X的样本编号对照表如下:
| X | 2 | 8 | 0 | 4 | 1 | 9 | 9 | 0 |
| 簇编号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
根据表可以知道,簇编号为5、6代表的样本就是两个位置为9的样本
同时,编号5、6的簇又会聚类成会编号为8的新簇,同理,依次递推,编号2、7的样本又会聚类成会聚类成编号为9的新簇……结果如下所示:
| 进行聚类操作的簇编号 | 5、6 | 2、7 | 0、4 | 1、8 | 9、10 | 3、12 | 11、13 |
| 新聚类的簇编号 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
Z的前两列我已经通过表格说明了,但是相信很多人卡就卡在不知道第三列数据是怎么求的,
所以下面对Z的第三列数据进行说明:
重点来了!!!!
第一行数据:由第一个表可知编号为5、6的簇,且都仅包含一个样本,所以样本的位置就代表簇的位置,因此两簇的位置都是9,两簇的距离![]()
第二行数据:由第一个表可知编号为2、7的簇,且都仅包含一个样本,所以样本的位置就代表簇的位置,因此两簇的位置都是0,两簇距离![]()
第三行数据:由第一个表可知编号为0、4的簇,且都仅包含一个样本,所以样本的位置就代表簇的位置,因此两簇的位置分别是2和1,两簇的距离![]()
第四行数据:由第一个表可知编号为1簇仅有一个样本,由表二可知编号为8的簇是由簇5和簇6聚类而来,其中含有两个样本,所以,为了计算簇1和簇8之间的距离,这时就需要用到上述所说到的ward算法的距离递推公式,计算流程如下:
![]()
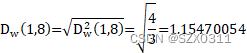
注意:Dw后面括号中的数字代表簇编号
第五行数据:由第二个表可知编号为9的簇是由簇2和簇7聚类而来,其中含有两个样本,编号为10的簇是由簇0和簇4聚类而来,其中含有两个样本,所以,为了计算簇9和簇10之间的距离,这时就需要用到上述所说到的ward算法的距离递推公式,计算流程如下:
![]()
![]()
![]()
所以:
![]()

因为比较懒,所以第六行与第七行中的第三列数据我就不再详细列计算过程了,大家看了第四行和第五行的计算过程应该也能明白如何使用ward的距离推导公式了
参考文章:
何晓群.多元统计分析(第五版)[M].中国人民大学出版社,2019.
Python层次聚类sci.cluster.hierarchy.linkage函数详解_scipy.cluster.hierarchy-CSDN博客
