当前位置： 首页 > news >正文

2.数据结构与算法 进阶知识

news 来源：原创 2024/5/19 1:09:57

文章目录

  • 数据结构与算法 (Python版)
    • 算法进阶
      • 知识点一 : 贪心算法
        • 1.贪心算法 概念
        • 2.贪心算法 找零问题
        • 3.贪心算法 背包问题
        • 4.贪心算法 拼接最大数字问题
        • 5.贪心算法 活动选择问题
      • 知识点二 : 动态规划
        • 1.动态规划 从斐波那契数列看动态规划
        • 2.动态规划 钢条切割问题
        • 3.动态规划 最长公共子序列
      • 知识点三 : 欧几里得算法
        • 1.最大公约数
        • 2.欧几里得算法实现四则运算
      • 知识点四 : RSA算法
        • 1. RSA算法介绍
        • 2.RSA加密算法过程

数据结构与算法 (Python版)

算法进阶

知识点一 : 贪心算法

1.贪心算法 概念

  • 贪心算法 (又称贪婪算法) 是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。
  • 贪心算法并不保证会得到最优解，但是在某些问题上贪心算法的解就是最优解。要会判断一个问题能否用贪心算法来计算。

  
  

2.贪心算法 找零问题

  • 假设商店老板需要找零n元钱，钱币的面额有:100元、50元、20元、5元、1元，如何找零使得所需钱币的数量最少?

    # -*- coding: utf-8 -*-

t = [100, 50, 20, 5, 1]


def change(t, n):
    m = [0 for _ in range(len(t))]
    for i, money in enumerate(t):
        m[i] = n // money
        n = n % money
    return m, n


print(change(t, 376))

  
  

3.贪心算法 背包问题

  • 一个小偷在某个商店发现有 n 个商品，第 i 个商品价值 vi 元，重 wi 千克。他希望拿走的价值尽量高，但他的背包最多只能容纳 W 千克的东西。他应该拿走哪些商品?

    • 0-1背包 : 对于一个商品，小偷要么把它完整拿走，要么留下。不能只拿走一部分，或把一个商品拿走多次。(商品为金条)
    • 分数背包:对于一个商品，小偷可以拿走其中任意一部分。(商品为金砂)

  • 举例 :

    • 商品1: v1=60 w1=10
    • 商品2∶v2=100 w2=20
    • 商品3∶V3=120 w3=30
    • 背包容量 : W=50

  • 代码实现

    # -*- coding: utf-8 -*-

goods = [(60, 10), (100, 20), (120, 30)]  # 每个商品元组表示(价格，重量)
goods.sort(key=lambda x: x[0]/x[1], reverse=True)


def fractional_backpack(goods, w):
    m = [0 for _ in range(len(goods))]
    total_v = 0
    for i, (prize, weight) in enumerate(goods):
        if w >= weight:
            m[i] = 1
            total_v += prize
            w -= weight
        else:
            m[i] = w / weight
            total_v += m[i] * prize
            w = 0
            break
    return total_v, m


print(fractional_backpack(goods, 50))

  
  

4.贪心算法 拼接最大数字问题

  • 有n个非负整数，将其按照字符串拼接的方式拼接为一个整数.如何拼接可以使得得到的整数最大?

    • 例如 : 32,94,128,1286,6,71 可以拼接除的最大整数为 94716321286128

  • 代码实现

    # -*- coding: utf-8 -*-

from functools import cmp_to_key

li = [32, 94, 128, 1286, 6, 71]


def xy_cmp(x, y):
    if x + y < y + x:
        return 1
    elif x + y > y + x:
        return -1
    else:
        return 0


def number_join(li):
    li = list(map(str, li))
    li.sort(key=cmp_to_key(xy_cmp))
    return "".join(li)


print(number_join(li))

  
  

5.贪心算法 活动选择问题

  • 假设有n个活动，这些活动要占用同一片场地,而场地在某时刻只能供一个活动使用。每个活动都有一个开始时间 s 和结束时间 f (题目中时间以整数表示),表示活动在[si, fi)区间占用场地。问:安排哪些活动能够使该场地举办的活动的个数最多?

    图片/数据结构与算法71.png

  • 贪心结论 : 最先结束的活动一定是最优解的一部分。

    • 证明 : 假设a是所有活动中最先结束的活动， b是最优解中最先结束的活动。
      • 如果a=b，结论成立。
      • 如果a≠b，则b的结束时间→十定晚于a的结束时间，则此时用a替换掉最优解中的b, a一定不与最优解中的其他活动时间重叠，因此替换后的解也是最优解。

  • 代码实现

    # -*- coding: utf-8 -*-

activities = [(1, 4), (3,5), (0, 6), (5, 7), (3,9), (5., 9), (6, 10), (8, 11), (8, 12), (2, 14), (12, 16)]
# 保证活动是按照结束时间排好序的
activities.sort(key=lambda x: x[1])


def activity_selection(a):
    res = [a[0]]
    for i in range(1, len(a)):
        if a[i][0] >= res[-1][1]:  # 当前活动的开始时间小于等于最后一个入选活动的结束时间
            # 不冲突
            res.append(a[i])
    return res


print(activity_selection(activities))

  
  

知识点二 : 动态规划

1.动态规划 从斐波那契数列看动态规划

  • 斐波那契数列 :Fn = Fn-1 + Fn-2

  • 使用递归和非递归的方法求解斐波那契数列的第n项

    # -*- coding: utf-8 -*-

# 子问题的重复计算
def fibnacci(n):
    if n == 1 or n == 2:
        return 1
    else:
        return fibnacci(n - 1) + fibnacci(n - 2)


# 动态规划 (DP) 的思想 = 最优子结构 (递推式)
def fibnacci_no_recurision(n):
    f = [0, 1, 1]
    if n > 2:
        for i in range(n - 2):
            num = f[-1] + f[-2]
            f.append(num)
    return f[n]


print(fibnacci_no_recurision(100))

  
  

2.动态规划 钢条切割问题

  • 某公司出售钢条，出售价格与钢条长度之间的关系如下表, 问题:现有一段长度为n的钢条和上面的价格表，求切割钢条方案，使得总收益最大。

    图片/数据结构与算法72.png

  • 长度为4的钢条的所有切割方案如下: (c方案最优)

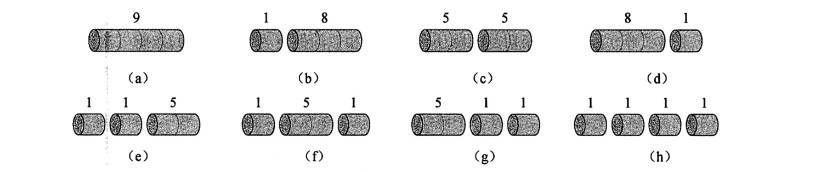
    图片/数据结构与算法73.png

    图片/数据结构与算法74.png

  • 钢条切割问题解决思路1:递推式

    • 设长度为n的钢条切割后最优收益值为n，可以得出递推式:

      • Tn = max(pn, T1 + Tn-1,r2 + Tn-2, … , Tn-1 + r1)

  • 第一个参数pn表示不切割

    • 其他n-1个参数分别表示另外n-1种不同切割方案，对方案i=1,2,…,n-1

      • 将钢条切割为长度为i和n-i两段

      • 方案i的收益为切割两段的最优收益之和

  • 考察所有的i，选择其中收益最大的方案

  • 钢条切割问题解决思路2: 最优子结构

    • 可以将求解规模为n的原问题，划分为规模更小的子问题:完成一次切割后，可以将产生的两段钢条看成两个独立的钢条切个问题。

    • 组合两个子问题的最优解，并在所有可能的两段切割方案中选取组合收益最大的，构成原问题的最优解。

    • 钢条切割满足最优子结构︰问题的最优解由相关子问题的最优解组合而成，这些子问题可以独立求解。

    • 钢条切割问题还存在更简单的递归求解方法

      • 从钢条的左边切割下长度为i的一段，只对右边剩下的一段继续进行切割，左
        边的不再切割

      • 递推式简化为

        图片/数据结构与算法75.png

      • 不做切割的方案就可以描述为︰左边一段长度为n，收益为pn，剩余一段长度为0，收益为r0=0。

  • 自顶向下实现代码

    # -*- coding: utf-8 -*-

import time


def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__, t2 - t1))
        return result

    return wrapper


p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]


# p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]

@cal_time
def cut_rod_recurision_1(p, n):
    if n == 0:
        return 0
    else:
        res = p[n]
        for i in range(1, n):
            res = max(res, cut_rod_recurision_1(p, i) + cut_rod_recurision_1(p, n - i))
        return res


# print(cut_rod_recurision_1(p, 9))

@cal_time
def c1(p, n):
    return cut_rod_recurision_1(p, n)


def cut_rod_recurision_2(p, n):
    if n == 0:
        return 0
    else:
        res = 0
        for i in range(1, n + 1):
            res = max(res, p[i] + cut_rod_recurision_2(p, n - i))
        return res


@cal_time
def c2(p, n):
    return cut_rod_recurision_2(p, n)


print(c1(p, 15))
print(c2(p, 15))

  • 自顶向上实现代码

    # -*- coding: utf-8 -*-

import time


def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__, t2 - t1))
        return result

    return wrapper


def cut_rod_recurision_2(p, n):
    if n == 0:
        return 0
    else:
        res = 0
        for i in range(1, n + 1):
            res = max(res, p[i] + cut_rod_recurision_2(p, n - i))
        return res


@cal_time
def c2(p, n):
    return cut_rod_recurision_2(p, n)


@cal_time
def cut_rod_dp(p, n):
    r = [0]
    for i in range(1, n + 1):
        res = 0
        for j in range(1, i + 1):
            res = max(res, p[j] + r[i - j])
        r.append(res)
    return r[n]


p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]

print(c2(p, 20))
print(cut_rod_dp(p, 15))

  • 重构解实现代码

    # -*- coding: utf-8 -*-

# -*- coding: utf-8 -*-

import time


def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__, t2 - t1))
        return result

    return wrapper


@cal_time
def cut_rod_dp(p, n):
    r = [0]
    for i in range(1, n + 1):
        res = 0
        for j in range(1, i + 1):
            res = max(res, p[j] + r[i - j])
        r.append(res)
    return r[n]


def cut_rod_extend(p, n):
    r = [0]
    s = [0]
    for i in range(1, n + 1):
        res_r = 0  # 价格的最大值
        res_s = 0  # 价格最大值对应方案的左边不切割部分的长度
        for j in range(1, i + 1):
            if p[j] + r[i - j] > res_r:
                res_r = p[j] + r[i - j]
                res_s = j
        r.append(res_r)
        s.append(res_s)
    return r[n], s


def cut_rod_solution(p, n):
    r, s = cut_rod_extend(p, n)
    ans = []
    while n > 0:
        ans.append(s[n])
        n -= s[n]
    return ans


p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]
r, s = cut_rod_extend(p, 20)
print(s)
print(cut_rod_dp(p, 20))
print(cut_rod_solution(p, 20))

  • 动态规划问题关键特征

    • 什么问题可以使用动态规划方法?
      • 最优子结构
        • 原问题的最优解中涉及多少个子问题
        • 在确定最优解使用哪些子问题时, 需要考虑多少种选择
      • 重叠子问题

  
  

3.动态规划 最长公共子序列

  • —个序列的子序列是在该序列中删去若干元素后得到的序列。例:“ABCD”和“BDF”都是“ABCDEFG”的子序列

  • 最长公共子序列(LCS)问题:给定两个序列X和Y，求X和Y长度最大的公共子序列。

    • 例:X="ABBCBDE” Y=“DBBCDB” LCS(×,Y)=“BBCD”

      图片/数据结构与算法76.png

    • 应用场景:字符串相似度比对

    • 例如:要求a="ABCBDAB"与b="BDCABA"的LCS :

      • 由于最后一位"B"≠"A":

        • 因此LcS(a,b)应该来源于LCS(a[:-1],b)与LCS(a,b[:-1])中
          更大的那一个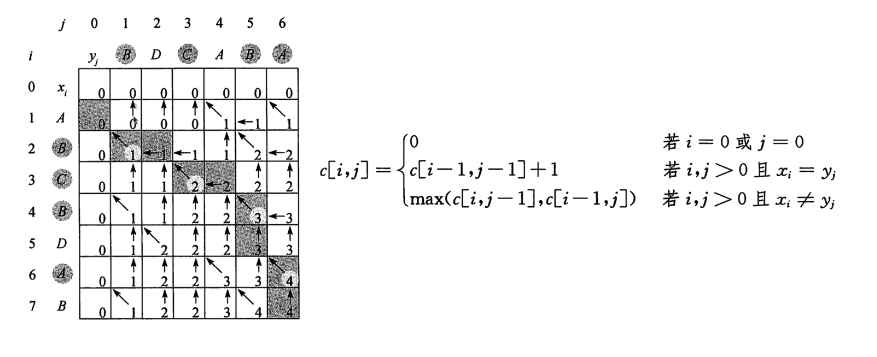

          图片/数据结构与算法77.png

  • 代码实现

    # -*- coding: utf-8 -*-

def lcs_length(x, y):
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if x[i - 1] == y[j - 1]:  # i j 位置上的字符匹配的时候, 来自于左上方+1
                c[i][j] = c[i - 1][j - 1] + 1
            else:
                c[i][j] = max(c[i - 1][j], c[i][j - 1])
    return c[m][n]


def lcs(x, y):
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    b = [[0 for _ in range(n + 1)] for _ in range(m + 1)]  # 1.左上方 2.上方 3.左方
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if x[i - 1] == y[j - 1]:  # i j 位置上的字符匹配的时候, 来自于左上方+1
                c[i][j] = c[i - 1][j - 1] + 1
                b[i][j] = 1
            elif c[i - 1][j] > c[i][j - 1]:  # 来自于上方
                c[i][j] = c[i - 1][j]
                b[i][j] = 2
            else:
                c[i][j] = c[i][j - 1]
                b[i][j] = 3
    return c[m][n], b


def lcs_trackback(x, y):
    c, b = lcs(x, y)
    i = len(x)
    j = len(y)
    res = []
    while i > 0 and j > 0:
        if b[i][j] == 1:  # 来自左上方->匹配
            res.append(x[i - 1])
            i -= 1
            j -= 1
        elif b[i][j] == 2:  # 来自于上方->不匹配
            i -= 1
        else:  # ==3 来自于左方->不匹配
            j -= 1
    return "".join(reversed(res))


# print(lcs_trackback("ABCBDAB", "BDCABA"))
c,b = lcs("ABCBDAB", "BDCABA")
for _ in b:
    print(_)

  
  

知识点三 : 欧几里得算法

1.最大公约数

  • 约数︰如果整数a能被整数b整除,那么a叫做b的倍数， b叫做a的约数。

  • 给定两个整数a,b，两个数的所有公共约数中的最大值即为最大公约数(Greatest Common Divisor, GCD) 。

    • 例:12与16的最大公约数是4

  • 如何计算两个数的最大公约数︰

    • 欧几里得:辗转相除法（欧几里得算法)
    • 《九章算术》︰更相减损术

  • 欧几里得算法: gcd(a, b)= gcd(b, a mod b)

    • 例: gcd(60,21) = gcd(21,18)= gcd(18,3)= gcd(3,O)= 3

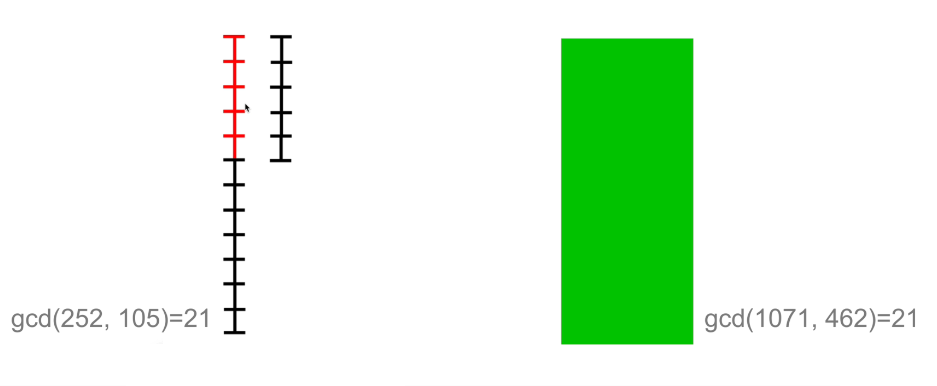
      图片/数据结构与算法78.png

  
  

2.欧几里得算法实现四则运算

  • 代码实现

    # -*- coding: utf-8 -*-

def gcd(a, b):
    if b == 0:
        return a
    else:
        return gcd(b, a % b)


def gcd2(a, b):
    while b > 0:
        r = a % b
        a = b
        b = r
    return a


# print(gcd2(12, 16))

class Fraction:
    def __init__(self, a, b):
        self.a = a
        self.b = b
        x = self.gcd(a, b)
        self.a /= x
        self.b /= x

    @staticmethod
    def gcd(a, b):
        while b > 0:
            r = a % b
            a = b
            b = r
        return a

    def zgs(self, a, b):
        # 12 16 ->4
        # 3*4*4=48
        x = gcd(a, b)
        return a * b / x

    def __add__(self, other):
        a = self.a
        b = self.b
        c = other.a
        d = other.b
        fenmu = self.zgs(b, d)
        fenzi = a * fenmu / b + c * fenmu / d
        return Fraction(fenzi, fenmu)

    def __str__(self):
        return "%d/%d" % (self.a, self.b)


a = Fraction(1, 3)
b = Fraction(1, 2)
print(a+b)

  
  

知识点四 : RSA算法

1. RSA算法介绍

  • 传统密码︰加密算法是秘密的

  • 现代密码系统:加密算法是公开的，密钥是秘密的

    • 对称加密
    • 非对称加密

  • RSA非对称加密系统:

    • 公钥:用来加密，是公开的

    • 私钥︰用来解密，是私有的

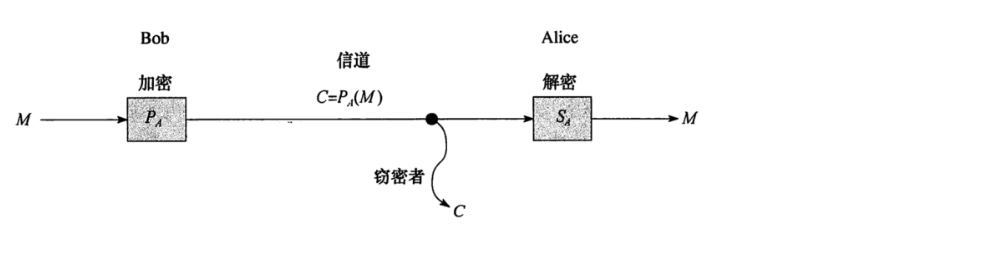
      图片/数据结构与算法79.png

2.RSA加密算法过程

  • RSA加密算法过程介绍
    • 1.随机选取两个质数p和q
    • 2.计算n=pq
    • 3.选取一个与p(n)互质的小奇数e,(n)=(p-1)(q-1)
    • 4.对模p(n),计算e的乘法逆元d，即满足(e*d) mod p(n)= 1
    • 5.公钥(e, n)私钥(d, n)
  • RSA加密算法过程介绍实现
    • 加密过程:c = (m^e) nod n
    • 解密过程:m = (c^d) mod n

相关文章：

  • 下载JDK8 JVM源码
  • 基于某钉探索针对CEF框架的一些逆向思路
  • C++迭代器
  • 关联容器(字典)map
  • 欧拉函数——最大公约数（gcd+筛质数+欧拉函数）
  • 【小程序】网络请求API介绍及网络请求的封装
  • ALTERA FPGA IPCORE核之单口RAM详细教程
  • Windows与网络基础-17-组策略应用
  • Python机器学习-多元分类的5种模型
  • k8s之client-go和ctrl的各种k8s client
  • 排序1：快速排序(三种)、归并排序、计数排序
  • LeetCode每日一题——1582. 二进制矩阵中的特殊位置
  • 【最长递增系列】动态规划法和贪心法
  • RabbitMQ入门与进阶实战
  • 【论文阅读】【yolo系列】YOLOV7的论文阅读
  • 《剑指offer》分解让复杂问题更简单
  • Android组件 - 收藏集 - 掘金
  • ECMAScript6(0)：ES6简明参考手册
  • Java｜序列化异常StreamCorruptedException的解决方法
  • Logstash 参考指南（目录）
  • Mybatis初体验
  • Odoo domain写法及运用
  • React-flux杂记
  • Redis中的lru算法实现
  • session共享问题解决方案
  • TypeScript迭代器
  • WePY 在小程序性能调优上做出的探究
  • 成为一名优秀的Developer的书单
  • 个人博客开发系列：评论功能之GitHub账号OAuth授权
  • 工作踩坑系列——https访问遇到“已阻止载入混合活动内容”
  • 力扣(LeetCode)22
  • 算法---两个栈实现一个队列
  • 通过git安装npm私有模块
  • 详解NodeJs流之一
  • 写给高年级小学生看的《Bash 指南》
  • 硬币翻转问题，区间操作
  • 自制字幕遮挡器
  • Spring Batch JSON 支持
  • 完善智慧办公建设，小熊U租获京东数千万元A+轮融资 ...
  • ​flutter 代码混淆
  • # 数论-逆元
  • # 学号 2017-2018-20172309 《程序设计与数据结构》实验三报告
  • #我与Java虚拟机的故事#连载18：JAVA成长之路
  • （第二周）效能测试
  • （附程序）AD采集中的10种经典软件滤波程序优缺点分析
  • （十三）Flask之特殊装饰器详解
  • （十三）Java springcloud B2B2C o2o多用户商城 springcloud架构 - SSO单点登录之OAuth2.0 根据token获取用户信息(4)...
  • （一）WLAN定义和基本架构转
  • （转）3D模板阴影原理
  • （转）eclipse内存溢出设置 -Xms212m -Xmx804m -XX:PermSize=250M -XX:MaxPermSize=356m
  • (转)Sql Server 保留几位小数的两种做法
  • *（长期更新）软考网络工程师学习笔记——Section 22 无线局域网
  • .h头文件 .lib动态链接库文件 .dll 动态链接库
  • .net core 控制台应用程序读取配置文件app.config
  • .net core 依赖注入的基本用发