数值分析期末复习
第一章 科学计算
误差
解题步骤
- 先求绝对误差:
∣ x − x ∗ ∣ |x - x^*| ∣x−x∗∣ - 求相对误差限:
∣ x − x ∗ ∣ x ∗ \frac{|x\,\,-\,\,x^*|}{x^*} x∗∣x−x∗∣ - 求有效数字
∣ x − x ∗ ∣ 需要小于它自身的半个单位 |x-x^*|\text{需要小于它自身的半个单位} ∣x−x∗∣需要小于它自身的半个单位,然后算小数点后一共有多少数字
举个例子:
相减得出结果为0.0000345则小于0.0005,则有效数字为4
例题1:

第二章 线性代数直接法
高斯消去法
高斯顺序消去法解题步骤
(假设是一个三行三列的矩阵):
- 先用第一行消去2,3行
- 再用第二行消去第三行
例题1:

例题2:

高斯列主元消去法解题步骤
- 比较哪一行的绝对值最大,然后交换
- 用第一行消去第2、3行
- 再次比较哪一行绝对值最大,交换
- 重复步骤
例题1:

例题2:


LU分解
LU分解又称为:杜利特尔 (Doolittle)分解法,直接三角分解法
解题步骤
- 将A矩阵分解成L、U矩阵
- L矩阵:下三角矩阵,对角线全为1,其他元素为x
- U矩阵:上三角矩阵,第一行元素和A矩阵相同,其他元素为x
- 从A中矩阵逆向推导,L、U剩下的元素逐一相乘得出结果
- 按照顺序一行一行的元素去算
例题1:



追赶法
追赶法又称为:克劳特分解
解题步骤
- 将A矩阵分解为L、U矩阵
- L矩阵的特点:下三角矩阵,对角线为未知数 α \alpha α,其他元素对A照抄
- U矩阵的特点:上三角矩阵,对角线为1,对角线上面的元素为 β \beta β
- 把 α , β \alpha,\beta α,β全部算出来
- L y = b Ly=b Ly=b -> U x = y Ux=y Ux=y
例题:



第三章 线性代数方程组的迭代法
范数和条件数
- 1范数(列范数):每一列元素的绝对值之和的最大值 ∣ ∣ A ∣ ∣ 1 ||A||_1 ∣∣A∣∣1
- 无穷范数(行范数):每一行元素的绝对值之和的最大值
- 2范数:
- 向量:向量元素平方的和的平方根
- 矩阵(又称为谱范数):null
- 无穷范数条件数:
c o n d ∞ ( A ) = ∣ ∣ A ∣ ∣ ∞ ∣ ∣ A − 1 ∣ ∣ ∞ cond_{\infty}\left( A \right) \,\,=\,\,||A||_{\infty}||A^{-1}||_{\infty} cond∞(A)=∣∣A∣∣∞∣∣A−1∣∣∞
例题1:

例题2:

求 A − 1 A^{-1} A−1的方法
- 初等变换法

雅可比迭代法
解题步骤
- 整体思路:将 Ax=b ->x=Bx+g 的形式
- 先将第一行转换为 x 1 = . . . x_1=... x1=...
- 第二行 x 3 = . . . . x_{3}= .... x3=....
- 以此类推
- 画出表格

计算器解题步骤
- 先将A、B、C、D、E、F设置为0 ( A 代表 x 1 , B 代表 x 2 , C 代表 x 3 A代表x_1,B代表x_2,C代表x_3 A代表x1,B代表x2,C代表x3)
- 0 sto A
- 0 sto B
- 0 sto C
- 0 sto D
- 0 sto E
- 0 sto F
- 将每一行公式输入到计算器中,使用 : : :进行分割
- D = …:E = …:F = …:A=D:B=E:C=F
- 这里是因为一开始不迭代,所以要设置DEF
- D = …:E = …:F = …:A=D:B=E:C=F
高斯迭代法
解题步骤
- 与雅可比迭代类似
- 但是每次都会迭代前面那个值
计算器解题步骤
- 先将A、B、C设置为0 ( A 代表 x 1 , B 代表 x 2 , C 代表 x 3 A代表x_1,B代表x_2,C代表x_3 A代表x1,B代表x2,C代表x3)
- 0 sto A
- 0 sto B
- 0 sto C
- 将每一行公式输入到计算器中,使用 : : :进行分割
- A = …:B = …:C = …
雅可比、高斯敛散性
1. 是否严格对角占优
严格对角占优:每一个对角元素的绝对值都大于它这一行的非对角元素绝对值之和,就是严格对角占优
2. 判断谱半径是否小于 1
- 计算 A 矩阵的L、D、U
A:

L: 下三角矩阵 L 包含 A 对角线以下的元素,其余位置为 0 (包括对角线)。 下三角矩阵 L 包含 A 对角线以下的元素,其余位置为0(包括对角线)。 下三角矩阵L包含A对角线以下的元素,其余位置为0(包括对角线)。
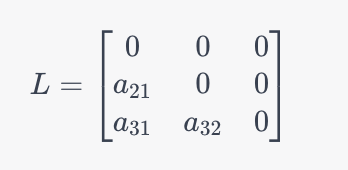
D: 对角矩阵 D 仅包含 A 的对角线元素,其余位置为 0 。 D − 1 是 D 每个元素的倒数 对角矩阵 D 仅包含 A 的对角线元素,其余位置为0。D^{-1}是D 每个元素的倒数 对角矩阵D仅包含A的对角线元素,其余位置为0。D−1是D每个元素的倒数

U: 上三角矩阵 U 包含 A 对角线以上的元素,其余位置为 0 (包括对角线)。 上三角矩阵 U 包含 A 对角线以上的元素,其余位置为0(包括对角线)。 上三角矩阵U包含A对角线以上的元素,其余位置为0(包括对角线)。
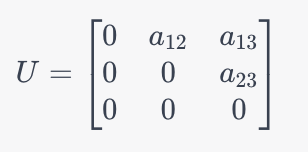
- 计算迭代矩阵 T J = − D − 1 ( L + U ) 计算迭代矩阵 T_J=-D^{-1}(L+U) 计算迭代矩阵TJ=−D−1(L+U)
- 计算出谱半径:特征值绝对值的最大值 如果小于1 则收敛否则不收敛
用计算器计算特征值
-
特征值回顾:
-
矩阵赋值 将 ANS 赋值给 B
-
∣ A − λ E ∣ = 0 ,算出 λ 1 、 λ 2 、 λ 3 |A-\lambda E| = 0 , 算出 \lambda_{1} 、 \lambda_{2} 、\lambda_3 ∣A−λE∣=0,算出λ1、λ2、λ3
-
再计算出 ( A − λ E ) = 0 (A-\lambda E) = 0 (A−λE)=0
- 化到最简 ( A − λ E ) (A-\lambda E) (A−λE)
第四章 多项式插值和样条插值
拉格朗日插值
一共 2 个部分:
- 插值多项式
- 插值余项
插值多项式
- l n ( x ) = [ ∏ i = 0 , i ≠ j n x − x i x j − x i ] y i l_n(x) =[ \prod_{i=0,i\ne j}^{n}\frac{x-x_i}{x_j-xi}] y_i ln(x)=[∏i=0,i=jnxj−xix−xi]yi
- L n ( x ) = ∑ j = 0 n L j ( x ) y j L_n(x)=\sum_{j=0}^{n}L_j(x)y_j Ln(x)=∑j=0nLj(x)yj
线性 n=1,以此类推后面就是 2 次、3 次
插值余项
- ∣ R n ( x ) ∣ = M n + 1 ( n + 1 ) ! ∣ W n + 1 ( x ) ∣ |R_n(x)|=\frac{M_{n+1}}{(n+1)!} |W_{n+1}(x)| ∣Rn(x)∣=(n+1)!Mn+1∣Wn+1(x)∣
- M n + 1 = max a ≤ x ≤ b ∣ f n + 1 ( x ) ∣ M_{n+1} = \max_{a\le x\le b}|f^{n+1}(x)| Mn+1=maxa≤x≤b∣fn+1(x)∣
- W n + 1 ( x ) = ( x − x 0 ) ( x − x 1 ) . . . ( x − x n ) W_{n+1}(x) = (x-x_0)(x-x_1)...(x-x_n) Wn+1(x)=(x−x0)(x−x1)...(x−xn)
牛顿插值
插值多项式
- f ( x 0 , . . . , x n ) = f n − f n − 1 x n − x 0 f(x_0,...,x_n) = \frac{f_n - f_{n-1}}{x_n-x_0} f(x0,...,xn)=xn−x0fn−fn−1
解题步骤
- 列差商表
| x | f(x) | 一阶差商 |
|---|---|---|
| x 0 x_0 x0 | f 0 f_0 f0 | |
| x 1 x_1 x1 | f 1 f_1 f1 | f ( x 0 , x 1 ) f(x_0,x_1) f(x0,x1) |
以此类推,有 n 个 x 的值就有多少次 n-1 阶差商
- 最后的结果公式
N n ( x ) = f 0 + f ( x 0 , x 1 ) ( x − x 0 ) + . . . + f ( x 0 , . . . , x n + 1 ) ( x − x 0 ) ( x − x 1 ) . . . ( x − x n ) N_{n}(x)=f_0 + f(x_0,x_1)(x-x_0) +...+f(x_0,...,x_{n+1})(x-x_0)(x-x_1)...(x-x_n) Nn(x)=f0+f(x0,x1)(x−x0)+...+f(x0,...,xn+1)(x−x0)(x−x1)...(x−xn)
牛顿插值余项
需要补充
第五章 函数逼近
最佳平方逼近
解题步骤
- 一般题目会给多项式,将其改写为 y = a + b x + c x 2 + d x 3 + . . . y = a + bx + cx^{2}+ dx^{3}+ ... y=a+bx+cx2+dx3+...,还有区间 [ u , d ] [u,d] [u,d]
- 如果是线性最佳平方逼近 多项式为 y = a + b x y= a+ bx y=a+bx
- 这边 φ 0 = 1 \varphi_{0}= 1 φ0=1代表第一个未知数, φ 1 = x , φ 2 = x 2 , φ 3 = x 3 \varphi_{1}= x,\varphi_{2}= x^{2} ,\varphi_{3}=x^3 φ1=x,φ2=x2,φ3=x3
- 列法方程
- ( ( φ 0 , φ 0 ) ( φ 0 , φ 1 ) ( φ 0 , φ 2 ) ( φ 1 , φ 0 ) ( φ 1 , φ 1 ) ( φ 1 , φ 2 ) ( φ 2 , φ 0 ) ( φ 2 , φ 1 ) ( φ 2 , φ 2 ) ( a b c ) = ( ( f , φ 0 ) ( f , φ 1 ) ( f , φ 2 ) ) \begin{pmatrix}(\varphi_0,\varphi_0) & (\varphi_0,\varphi_1) & (\varphi_0,\varphi_2)\\ (\varphi_1,\varphi_0) & (\varphi_1,\varphi_1) & (\varphi_1,\varphi_2)\\ (\varphi_2,\varphi_0) & (\varphi_2,\varphi_1)&(\varphi_2,\varphi_2\end{pmatrix} \begin{pmatrix}a \\b \\c\end{pmatrix} = \begin{pmatrix}(f,\varphi_0) \\(f,\varphi_1) \\(f,\varphi_2)\end{pmatrix} (φ0,φ0)(φ1,φ0)(φ2,φ0)(φ0,φ1)(φ1,φ1)(φ2,φ1)(φ0,φ2)(φ1,φ2)(φ2,φ2 abc = (f,φ0)(f,φ1)(f,φ2)
- 第一个位置以 φ 0 开始,后面每一行开头都自增,第二个位置从 φ 0 到 φ n 结束 第一个位置以\varphi_0开始,后面每一行开头都自增,第二个位置从\varphi_0到\varphi_n结束 第一个位置以φ0开始,后面每一行开头都自增,第二个位置从φ0到φn结束
- a,b,c 是多项式中的 a,b,c
- f 为 y
- 计算
- ( φ 0 , φ 0 ) (\varphi_0,\varphi_0) (φ0,φ0) => ∫ d u φ 0 ∗ φ 0 d x \int_{d}^{u} \varphi_0 * \varphi_0 dx ∫duφ0∗φ0dx
- ( f , φ 0 ) (f,\varphi_0) (f,φ0) => ∫ d u f ∗ φ 0 d x \int_{d}^{u} f* \varphi_0 dx ∫duf∗φ0dx
- 以此类推
- 算出方程后直接代入计算器解出 a,b,c 的值
最小二乘法
解题步骤:
- 通常使用最小二乘法都会带有 x,y 的表格和一个多项式
- 化简多项式为: φ 0 = 1 , φ 1 = x , φ 2 = x 2 , φ 3 = x 3 和 a , b , c 的形式 \varphi_{0}= 1,\varphi_{1}= x,\varphi_{2}= x^{2} ,\varphi_{3}=x^{3}和 a,b,c 的形式 φ0=1,φ1=x,φ2=x2,φ3=x3和a,b,c的形式
- 列法方程
- 计算前先举个例子:
-
y = a + b x y=a + bx y=a+bx -> 这里 φ 0 = 1 , φ 1 = x \varphi_{0}= 1,\varphi_{1} = x φ0=1,φ1=x
x有 3 个,那么 φ 0 = [ 1 1 1 ] \varphi_{0}= \begin{bmatrix} 1\\1 \\1\end{bmatrix} φ0= 111 ,将 x 代入, φ 1 = [ − 3 − 2 − 1 ] \varphi_{1}= \begin{bmatrix} -3\\-2 \\-1\end{bmatrix} φ1= −3−2−1
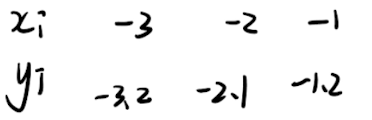
如果有 φ 2 = x 2 \varphi_{2} = x^2 φ2=x2的话,那么 φ 2 = [ ( − 3 ) 2 = 9 ( − 2 ) 2 = 4 ( − 1 ) 2 = 1 ] \varphi_{2} = \begin{bmatrix} (-3)^2 = 9\\(-2) ^ 2 =4 \\ (-1)^2 = 1\end{bmatrix} φ2= (−3)2=9(−2)2=4(−1)2=1
-
建立法方程:
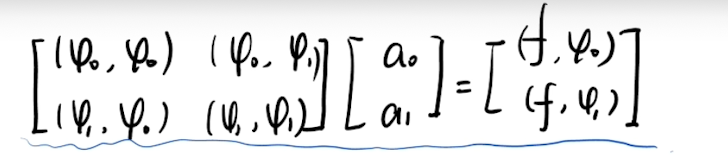
-
( φ 0 , φ 0 ) (\varphi_0,\varphi_0) (φ0,φ0)
- x 个 1 组成的向量内积和 x 个 1 组成的向量内积和 x个1组成的向量内积和
- [ 1 1 1 ] ∗ [ 1 1 1 ] = 1 + 1 + 1 = 3 \begin{bmatrix}1 \\1 \\1\end{bmatrix} * \begin{bmatrix}1 \\1 \\1\end{bmatrix} =1 + 1 + 1 =3 111 ∗ 111 =1+1+1=3
- x 个 1 组成的向量内积和 x 个 1 组成的向量内积和 x个1组成的向量内积和
-
( φ 0 , φ 1 ) (\varphi_0,\varphi_1) (φ0,φ1) = ( φ 1 , φ 0 ) (\varphi_1,\varphi_0) (φ1,φ0) = [ 1 1 1 ] ∗ [ − 3 − 2 − 1 ] = − 3 + ( − 2 ) + ( − 1 ) = − 6 \begin{bmatrix} 1\\1 \\1\end{bmatrix} * \begin{bmatrix} -3\\-2 \\-1\end{bmatrix} = -3 + (-2) + (-1) = -6 111 ∗ −3−2−1 =−3+(−2)+(−1)=−6
-
( φ 1 , φ 1 ) (\varphi_1,\varphi_1) (φ1,φ1) = [ − 3 − 2 − 1 ] ∗ [ − 3 − 2 − 1 ] = 9 + 4 + 1 = 14 \begin{bmatrix} -3\\-2 \\-1\end{bmatrix} * \begin{bmatrix} -3\\-2 \\-1\end{bmatrix} = 9 + 4 + 1 = 14 −3−2−1 ∗ −3−2−1 =9+4+1=14
-
( f , φ 1 ) = [ − 3.2 − 2.1 − 1.2 ] ∗ [ − 3 − 2 − 1 ] = ( − 3 ∗ ( − 3.2 )) + ( − 2.1 ∗ ( − 2 )) + ( − 1.2 + ( − 1 )) = 15 (f,\varphi_1) = \begin{bmatrix} -3.2\\-2.1 \\-1.2\end{bmatrix} * \begin{bmatrix}-3 \\-2 \\-1\end{bmatrix} = (-3*(-3.2)) + (-2.1 * (-2)) + (-1.2 + (-1))=15 (f,φ1)= −3.2−2.1−1.2 ∗ −3−2−1 =(−3∗(−3.2))+(−2.1∗(−2))+(−1.2+(−1))=15
-
-
- 将值代入矩阵,通过计算器得出结果,将 a , b a,b a,b 结果代入 y = a + b x y=a + bx y=a+bx 得到最小二乘拟合函数
第九章 常微分方程初边值问题数值解
龙格-库塔公式
基本概念
一般问题会有 y ′ , h , f ( x ) = y y', h , f(x) = y y′,h,f(x)=y等参数
将其转换为
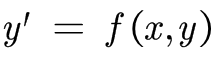
注意h的值,一般是在 0 ≤ x ≤ 1 0 \le x \le 1 0≤x≤1之间,逐渐相加之后递增到1结束计算
四阶四段龙格库塔公式如下:
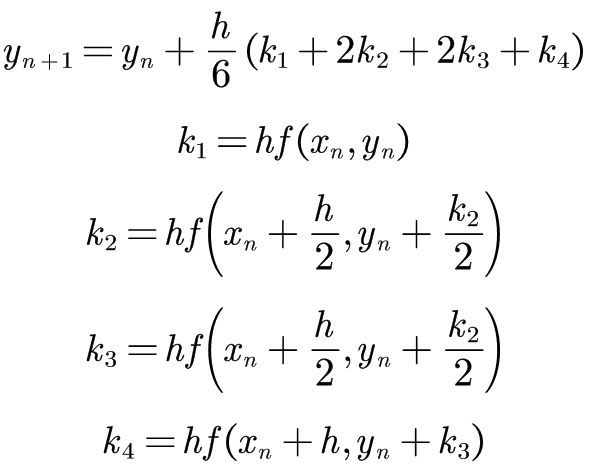
解题步骤
- 将 x 0 , y 0 , h x_0,y_0,h x0,y0,h写在旁边
- 先将题目中给出的已知信息代入 k 1 , k 2 , k 3 , k 4 k_1,k_2,k_3,k_4 k1,k2,k3,k4
- 更新 y n y_n yn的值
- 重复过程
k 2 k_2 k2->f的 x n + h 2 x_n+\frac{h}{2} xn+2h表示 x x x,同理另外一个表示 y y y,将其代入到f(x,y)中进行化简