当前位置：首页 > news >正文

计算电磁学：FDFD算法总结

news 来源：原创 2024/9/28 23:01:59

FDFD(Finite Difference Frequency Domain)在Yee格子上使用有限差分求解频域Maxwell方程组。本文通过FDFP差分方程组的推导来阐述FDFP的原理。

注1：限于研究水平，分析难免不当，欢迎批评指正。

注2：文章内容会不定期更新。

0、预修

0.1 Fourier变换及其逆变换

对于函数 $f\left ( t \right )$ ，如果在整个实数域 $\mathbb{R}$ 上绝对可积，即满足 $\int_{-\infty }^{+\infty }\left |f\left ( t \right ) \right |dt < \infty$ ，则存在Fourier变换 $F\left ( \omega \right )=\int_{-\infty }^{+\infty }f\left ( t \right )e^{-j\omega t}dt$ ，对应的Fourier逆变换为 $f\left ( t\right )=\frac{1}{2\pi }\int_{-\infty }^{+\infty }F\left ( \omega \right )e^{j\omega t}d\omega$ 。

一、数学模型

对于微分形式的Maxwell方程组，有

$\left\{\begin{matrix} \nabla \cdot \mathbf{D}=\rho\\ \nabla\cdot \mathbf{B}=0\\ \nabla\times \mathbf{H}=\boldsymbol{J}+\frac{\partial \boldsymbol{D}}{\partial t}\\ \nabla\times \mathbf{E}=-\frac{\partial \boldsymbol{B}}{\partial t}-\boldsymbol{M} \end{matrix}\right.$

依据Fourier逆变换，可得复数形式的Maxwell方程组，

$\left\{\begin{matrix} \nabla \cdot \mathbf{D}=\rho\\ \nabla\cdot \mathbf{B}=0\\ \nabla\times \mathbf{H}=\boldsymbol{J}+j\omega\boldsymbol{D}\\ \nabla\times \mathbf{E}=-j\omega\boldsymbol{B}-\boldsymbol{M} \end{matrix}\right.$

对于各向异性介质，则有

$\left\{\begin{matrix} \nabla \cdot \mathbf{D}=\rho\\ \nabla\cdot \mathbf{B}=0\\ \nabla\times \mathbf{H}=\boldsymbol{J}+j\omega\boldsymbol{\epsilon}\cdot \boldsymbol{E}\\ \nabla\times \mathbf{E}=-j\omega\boldsymbol{\mu}\cdot \boldsymbol{H}-\boldsymbol{M} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} \boldsymbol{\mu}^{-1}\nabla^{2} \boldsymbol{E}+\omega ^{2}\boldsymbol{\epsilon}\cdot\boldsymbol{E}=\nabla\times \boldsymbol{\mu}^{-1}\cdot \nabla\times\boldsymbol{E}+\boldsymbol{\mu}^{-1}\nabla\nabla\cdot \boldsymbol{E}+j\omega\boldsymbol{J}+\nabla\times\boldsymbol{\mu}^{-1}\cdot \boldsymbol{M}\\ \boldsymbol{\epsilon}^{-1}\nabla^{2} \boldsymbol{H}+\omega ^{2}\boldsymbol{\mu}\cdot\boldsymbol{H}=\nabla\times \boldsymbol{\epsilon}^{-1}\cdot \nabla\times\boldsymbol{H}+\boldsymbol{\epsilon}^{-1}\nabla\nabla\cdot \boldsymbol{H}+j\omega\boldsymbol{M}-\nabla\times\boldsymbol{\epsilon}^{-1}\cdot \boldsymbol{J}\end{matrix}\right.$

不考虑电流密度 $\boldsymbol{J}$ 与磁流密度 $\boldsymbol{M}$ ，在均匀各向同性介质中，有

$\left\{\begin{matrix}\nabla\times \mathbf{H}=j\omega \epsilon \boldsymbol{E} \\ \nabla\times\mathbf{E}=-j\omega \mu \boldsymbol{H} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} \nabla^{2}\boldsymbol{H}+\omega ^{2}\epsilon\mu\boldsymbol{H}=0\\ \nabla^{2}\boldsymbol{E}+\omega ^{2}\epsilon\mu\boldsymbol{E}=\frac{\nabla\rho }{\epsilon}\end{matrix}\right.$

在笛卡尔直角坐标系下，有

$\left\{\begin{matrix} \frac{\partial H_{z}}{\partial y}-\frac{\partial H_{y}}{\partial z}=j\omega \epsilon E_{x}\\ \frac{\partial H_{x}}{\partial z}-\frac{\partial H_{z}}{\partial x}=j\omega \epsilon E_{y}\\ \frac{\partial H_{y}}{\partial x}-\frac{\partial H_{x}}{\partial y}=j\omega \epsilon E_{z}\end{matrix}\right.$ $\left\{\begin{matrix} \frac{\partial E_{z}}{\partial y}-\frac{\partial E_{y}}{\partial z}=-j\omega \mu H_{x}\\ \frac{\partial E_{x}}{\partial z}-\frac{\partial E_{z}}{\partial x}=-j\omega \mu H_{y}\\ \frac{\partial E_{y}}{\partial x}-\frac{\partial E_{x}}{\partial y}=-j\omega \mu H_{z}\end{matrix}\right.$

二、数值模型：控制方程的空间离散

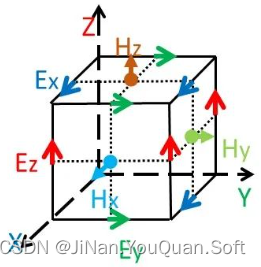
FDFD算法也采用Yee格子在空间上进行离散。在Yee格子中，电场分量放置到Yee单元各棱的中间，方向平行于各棱；磁场分量放置到Yee单元各面中心，方向平行于各面法线。

$\left\{\begin{matrix} \frac{H_{z}\left (i+\frac{1}{2},j+\frac{1}{2},k \right )-H_{z}\left (i+\frac{1}{2},j-\frac{1}{2},k \right )}{\Delta y}-\frac{H_{y}\left (i+\frac{1}{2},j,k+\frac{1}{2} \right )-H_{y}\left (i+\frac{1}{2},j,k-\frac{1}{2} \right )}{\Delta z}=j\omega \epsilon E_{x}\left ( i+\frac{1}{2},j,k \right )\\ \frac{H_{x}\left (i,j+\frac{1}{2},k+\frac{1}{2} \right )-H_{x}\left (i,j+\frac{1}{2},k-\frac{1}{2} \right )}{\Delta z}-\frac{H_{z}\left (i+\frac{1}{2},j+\frac{1}{2},k \right )-H_{z}\left (i-\frac{1}{2},j+\frac{1}{2},k \right )}{\Delta x}=j\omega \epsilon E_{y}\left ( i,j+\frac{1}{2},k \right )\\ \frac{H_{y}\left (i+\frac{1}{2},j,k+\frac{1}{2} \right )-H_{y}\left (i-\frac{1}{2},j,k+\frac{1}{2} \right )}{\Delta x}-\frac{H_{x}\left (i,j+\frac{1}{2},k+\frac{1}{2} \right )-H_{x}\left (i,j-\frac{1}{2},k+\frac{1}{2} \right )}{\Delta y}=j\omega \epsilon E_{z}\left ( i,j,k+\frac{1}{2} \right ) \end{matrix}\right.$

$\left\{\begin{matrix} \frac{E_{z}\left (i,j+1,k+\frac{1}{2} \right )-E_{z}\left (i,j,k+\frac{1}{2} \right )}{\Delta y}-\frac{E_{y}\left (i,j+\frac{1}{2},k+1 \right )-E_{y}\left (i,j+\frac{1}{2},k \right )}{\Delta z}=-j\omega \mu H_{x}\left ( i,j+\frac{1}{2},k+\frac{1}{2} \right )\\ \frac{E_{x}\left (i+\frac{1}{2},j,k+1 \right )-E_{x}\left (i+\frac{1}{2},j,k \right )}{\Delta z}-\frac{E_{z}\left (i+1,j,k+\frac{1}{2}\right )-E_{z}\left (i,j,k+\frac{1}{2} \right )}{\Delta x}=-j\omega \mu H_{y}\left ( i+\frac{1}{2},j,k+\frac{1}{2} \right )\\ \frac{E_{y}\left (i+1,j+\frac{1}{2},k \right )-E_{y}\left (i,j+\frac{1}{2},k \right )}{\Delta x}-\frac{E_{x}\left (i+\frac{1}{2},j+1,k\right )-E_{x}\left (i+\frac{1}{2},j,k \right )}{\Delta y}=-j\omega \mu H_{z}\left ( i+\frac{1}{2},j+\frac{1}{2},k \right )\end{matrix}\right.$

设 $n_{x}$ 、 $n_{y}$ 、 $n_{z}$ 分别表示 $x$ 、 $y$ 、 $z$ 方向上的Yee格子数目，考虑将上述差分方程组写成矩阵方程组 $\boldsymbol{A}\boldsymbol{X}$ 形式，则有，

$n=kn_{x}n_{y}+jn_{x}+i$

$A\left ( 6n,6n+4-6n_{x}n_{y} \right )=-\frac{1}{\Delta z}$ ， $A\left ( 6n,6n+5-6n_{x} \right )=\frac{1}{\Delta y}$ ， $A\left ( 6n,6n \right )=j\omega \epsilon$ ， $A\left ( 6n,6n+1 \right )=0$ ， $A\left ( 6n,6n+2 \right )=0$ ， $A\left ( 6n,6n+3 \right )=0$ ， $A\left ( 6n,6n+4 \right )=\frac{1}{\Delta z}$ ， $A\left ( 6n,6n+5 \right )=-\frac{1}{\Delta y}$

$A\left ( 6n+1,6n+3-6n_{x}n_{y} \right )=\frac{1}{\Delta z}$ ， $A\left ( 6n+1,6n-1\right )=-\frac{1}{\Delta x}$ ， $A\left ( 6n+1,6n \right )=0$ ， $A\left ( 6n+1,6n+1 \right )=j\omega \epsilon$ ， $A\left ( 6n+1,6n+2 \right )=0$ ， $A\left ( 6n+1,6n+3 \right )=-\frac{1}{\Delta z}$ ， $A\left ( 6n+1,6n+5 \right )=\frac{1}{\Delta x}$

$A\left ( 6n+2,6n+3-6n_{x} \right )=-\frac{1}{\Delta y}$ ， $A\left ( 6n+2,6n-2 \right )=\frac{1}{\Delta x}$ ， $A\left ( 6n+2,6n \right )=0$ ， $A\left ( 6n+2,6n+1 \right )=0$ ， $A\left ( 6n+2,6n+2 \right )=j\omega \epsilon$ ， $A\left ( 6n+2,6n+3 \right )=\frac{1}{\Delta y}$ ， $A\left ( 6n+2,6n+4 \right )=-\frac{1}{\Delta x}$

$A\left ( 6n+3,6n \right )=0$ ， $A\left ( 6n+3,6n+1 \right )=\frac{1}{\Delta z}$ ， $A\left ( 6n+3,6n+2 \right )=\frac{1}{\Delta y}$ ， $A\left ( 6n+3,6n+3 \right )=j\omega \mu$ ， $A\left ( 6n+3,6n+4\right )=0$ ， $A\left ( 6n+3,6n+5\right )=0$ ， $A\left ( 6n+3,6n+1+6n_{x} \right )=\frac{1}{\Delta y}$ ， $A\left ( 6n+3,6n+1+6n_{x}n_{y} \right )=-\frac{1}{\Delta z}$

$A\left ( 6n+4,6n\right )=-\frac{1}{\Delta z}$ ， $A\left ( 6n+4,6n+2 \right )=\frac{1}{\Delta x}$ ， $A\left ( 6n+4,6n+3 \right )=0$ ， $A\left ( 6n+4,6n+4 \right )=j\omega \mu$ ， $A\left ( 6n+4,6n+5 \right )=0$ ， $A\left ( 6n+4,6n+8 \right )=-\frac{1}{\Delta x}$ ， $A\left ( 6n+4,6n+6n_{x}n_{y}\right )=\frac{1}{\Delta z}$

$A\left ( 6n+5,6n \right )=\frac{1}{\Delta y}$ ， $A\left ( 6n+5,6n+2\right )=-\frac{1}{\Delta x}$ ， $A\left ( 6n+5,6n+3 \right )=0$ ， $A\left ( 6n+5,6n+4 \right )=0$ ， $A\left ( 6n+5,6n+5 \right )=j\omega \mu$ ， $A\left ( 6n+5,6n+8\right )=\frac{1}{\Delta x}$ ， $A\left ( 6n+5,6n+6n_{y} \right )=-\frac{1}{\Delta y}$