【控制实践——四旋翼无人机】【一】四旋翼无人机运动分析和建模
传送门
- 系列博客
- 前言
- 坐标系定义及姿态位置描述
- 坐标系定义
- 姿态描述及坐标系变换
- 受力分析
- 牛顿-欧拉方程
- 状态空间方程
- 总结
系列博客
前言
在C站摸爬滚打一段时间后,发现控制类相关的圈子较小(话题热度低),想顺便跟各位同行读者了解一些喜好。
平时在检索这方面资料信息时,通常采用什么渠道或者通过什么平台获得。有什么好的建议意见,欢迎私聊或评论。
在初学入门阶段,本人也会在c站搜索一些相关的内容,但总感觉信息繁复琐碎,要么过于保姆级别,内容简单但不利于深入理解,要么过于潦草敷衍,公式原理推导含糊不明,以致学习效率低下,甚至片面理解和误解。因此在撰写博客前,总结出自己的一些理解:
首先,要系统性的从原理出发进行推导(需要具备基础物理和数学知识,有一定的门槛!)
其次,借助仿真工具验证公式推导合理性
最后,通过实物实践再次论证(需要有很好的动手能力和实验思维!)
回到正题,在现在大环境下,对于自动化控制类的同学来说,四旋翼无人机已经成为必备技能之一。也搜索过C站的四旋翼相关博客,个人认为相对比较片面。因此决定开一个新的四旋翼控制的系列,结合一些四旋翼论文,系统性地分析四旋翼控制原理,并设计实物进行验证。
坐标系定义及姿态位置描述
坐标系定义
这一步是所有机器人控制的前提,因为所有的运动都可以认为是相对的,又是绝对的,随着参考对象的变化,也会得到不同的答案。因此明确坐标系定义,就明确了运动的相对性,并且能够定义运动的指标。
在飞行器的运动中,通常定义机体坐标系(非惯性系)和地球坐标系(惯性系)。
“为什么通常是这两个,不能是其他的”
“因为这两个能够简单高效地达到飞行器运动描述的目的。”
以上是我入门时杠过的一个问题。
机体系是根据飞行器结构定义的,是固连于飞行器的结构上的;
地球系是以地球为参考系建立的惯性坐标系,是固连于地球表面的,通常指向东北天。
在进行运动描述时,通常将飞行器视作刚体(其结构不会发生变形,质心位置不会发生变化),这是两个理想假设,通常会变化但是不会特别大。
因此,飞行器的位置,就可以通过飞行器质心点在地球系中的坐标点( x , y , z x,y,z x,y,z)来表示。这就完成了飞行器平动运动的描述。
同时,飞行器的姿态也很关键,因为他决定了四个螺旋桨的推力方向,是实现飞行器控制的关键状态信息。因此也需要有一些变量来描述这个转动运动。这里用到了机体系和地球系的相对角度位置来表述。
这里讲的很墨迹,主要是考虑到刚入门的同学对于坐标系变换和姿态表述不理解,需要慢慢引导。
这方面有基础的同学可以跳过!
关于姿态表述的方式,并不是绝对的,有若干种表述的方式。但每种姿态表述都有一个坐标轴的前提定义。
即假设转动过程是按Z-Y-X(三个轴都是机体系的坐标轴)顺序进行:
- 转动前
- 先按机体系Z轴转动 ψ \boldsymbol{\psi} ψ
- 再绕Z轴转动后的机体系Y轴转动 θ \boldsymbol{\theta} θ
- 最后在前面的基础绕机体系X轴转动 ϕ \boldsymbol{\phi} ϕ
而这三个旋转的角度( ϕ , θ , ψ \boldsymbol{\phi,\theta,\psi} ϕ,θ,ψ)分别对应横滚角(
机体系X轴转动角度),俯仰角(机体系Y轴转动角度),航向角(机体系Z轴转动角度)。
- 你仔细思考应该会发现,如果转动顺序变化,不再是Z-Y-X,而是按照X-Y-Z,那么得到三个姿态角的几何意义也将不同,这也是我前面提到的姿态角是相对的,具有前提的意思。
- 坐标系变换是一个变换的结果而非过程,在进行坐标系变换的数学描述时尤其体现这一点,到这里会有点抽象,之前看到B站上有一个不错的视频,链接
姿态描述及坐标系变换
这里我不想赘述,我之前有一篇博客做过相关推导。
Mahony姿态解算——坐标系变换
里面姿态角的符号不对应,但推导过程不变!
本文的坐标系旋转顺序是 Z − > Y − > X Z->Y->X Z−>Y−>X
由机体系到地球系的坐标系转换矩阵为 R \boldsymbol{R} R
R = [ C ψ C θ C ψ S θ S ϕ − S ψ C ϕ C ψ S θ C ϕ + S ψ S ϕ S ψ C θ S ψ S θ S ϕ + C ψ C ϕ S ψ S θ C ϕ − C ψ S ϕ − S θ C θ S ϕ C θ C ϕ ] \boldsymbol{R}=\left[\begin{array}{ccc} C_{\psi} C_{\theta} & C_{\psi} S_{\theta} S_{\phi}-S_{\psi} C_{\phi} & C_{\psi} S_{\theta} C_{\phi}+S_{\psi} S_{\phi} \\ S_{\psi} C_{\theta} & S_{\psi} S_{\theta} S_{\phi}+C_{\psi} C_{\phi} & S_{\psi} S_{\theta} C_{\phi}-C_{\psi} S_{\phi} \\ -S_{\theta} & C_{\theta} S_{\phi} & C_{\theta} C_{\phi} \end{array}\right] R= CψCθSψCθ−SθCψSθSϕ−SψCϕSψSθSϕ+CψCϕCθSϕCψSθCϕ+SψSϕSψSθCϕ−CψSϕCθCϕ
其中, ϕ \phi ϕ为横滚角, θ \theta θ为俯仰角, ψ \psi ψ为偏航角。 C x C_{x} Cx为对应角度的余弦值, S x S_{x} Sx为对应角度的正弦值。
设机体系的角速度向量为 ν = [ p q r ] \boldsymbol{\nu}=\begin{bmatrix}p\\q\\r\end{bmatrix} ν= pqr ,欧拉角向量 η = [ ϕ θ ψ ] \boldsymbol{\eta=\begin{bmatrix}\phi\\\theta\\\psi\end{bmatrix}} η= ϕθψ ,二者满足以下关系
η ˙ = W η − 1 ν , [ ϕ ˙ θ ˙ ψ ˙ ] = [ 1 S ϕ T θ C ϕ T θ 0 C ϕ − S ϕ 0 S ϕ / C θ C ϕ / C θ ] [ p q r ] \begin{array}{ll} \dot{\boldsymbol{\eta}}=\boldsymbol{W}_{\eta}^{-1} \boldsymbol{\nu}, & {\left[\begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right]=\left[\begin{array}{ccc} 1 & S_{\phi} T_{\theta} & C_{\phi} T_{\theta} \\ 0 & C_{\phi} & -S_{\phi} \\ 0 & S_{\phi} / C_{\theta} & C_{\phi} / C_{\theta} \end{array}\right]\left[\begin{array}{c} p \\ q \\ r \end{array}\right]} \end{array} η˙=Wη−1ν, ϕ˙θ˙ψ˙ = 100SϕTθCϕSϕ/CθCϕTθ−SϕCϕ/Cθ pqr
ν = W η η ˙ , [ p q r ] = [ 1 0 − S θ 0 C ϕ C θ S ϕ 0 − S ϕ C θ C ϕ ] [ ϕ ˙ θ ˙ ψ ˙ ] \begin{array}{ll} \boldsymbol{\nu}=\boldsymbol{W}_{\eta} \dot{\boldsymbol{\eta}}, & {\left[\begin{array}{c} p \\ q \\ r \end{array}\right]=\left[\begin{array}{ccc} 1 & 0 & -S_{\theta} \\ 0 & C_{\phi} & C_{\theta} S_{\phi} \\ 0 & -S_{\phi} & C_{\theta} C_{\phi} \end{array}\right]\left[\begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right]} \end{array} ν=Wηη˙, pqr = 1000Cϕ−Sϕ−SθCθSϕCθCϕ ϕ˙θ˙ψ˙
这里再标记一下,从上面的描述中可以看出,姿态角是过程量,不是结果量,即你无法直接从转动后的机体系中明确指出哪个角是横滚/俯仰/航向角。而且机体系的角速度,是指绕当前机体系坐标轴转动的速度。因此可以得到一个结论:
欧拉角的变化率不等于机体系的角速度
这里强调这个结论是因为我之前就是误解了二者的关系,造成很多后续的认知错误。
这里还要考虑矩阵不可逆的情况。
受力分析
飞行器的主动力有四个螺旋桨产生的力,主动扭矩只有四个螺旋桨产生的反扭矩。受力情况如图:
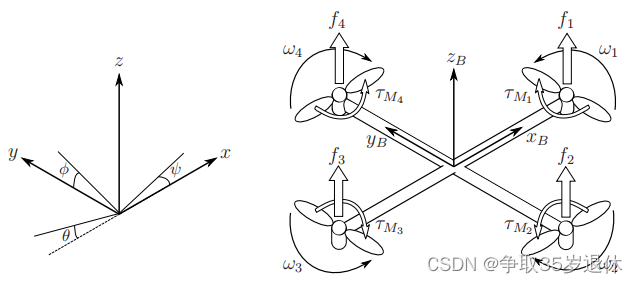
四个螺旋桨的力 f i , i = 1 , 2 , 3 , 4 \boldsymbol{f_{i},i=1,2,3,4} fi,i=1,2,3,4
f i = k ω i 2 \boldsymbol{f_{i}=k\omega_{i}^{2}} fi=kωi2
四个螺旋桨的反扭矩 τ M i , i = 1 , 2 , 3 , 4 \boldsymbol{\tau_{Mi},i=1,2,3,4} τMi,i=1,2,3,4
τ M i = b ω i 2 + I M ω ⋅ i \boldsymbol{\tau_{Mi}=b \omega_{i}^{2}+I_{M}\overset{\cdot}\omega_{i}} τMi=bωi2+IMω⋅i
通常由于螺旋桨转速变化产生的自转力矩较小,因此将其忽略,即
τ M i = b ω i 2 \boldsymbol{\tau_{Mi}=b \omega_{i}^{2}} τMi=bωi2
其中 ω i , i = 1 , 2 , 3 , 4 \boldsymbol{\omega_{i},i=1,2,3,4} ωi,i=1,2,3,4分别对应四个螺旋桨的转速
假设四旋翼机架四边对称,质心位置到四个螺旋桨的中心距离均为 l \boldsymbol{l} l,则可以得到螺旋桨产生的四旋翼推力 T T T为:
T = ∑ i = 1 4 f i = k ∑ i = 1 4 ω i 2 , T B = [ 0 0 T ] T=\sum_{i=1}^{4}{\boldsymbol{f_{i}}}=k\sum_{i=1}^{4}{\boldsymbol{\omega^{2}_{i}}},\boldsymbol{T}_{B}=\begin{bmatrix}0\\0\\T\end{bmatrix} T=i=1∑4fi=ki=1∑4ωi2,TB= 00T
同样,由螺旋桨所产生的四旋翼机体下的力矩矢量 τ B \boldsymbol{\tau_{B}} τB:
τ B = [ l k ( − ω 2 2 + ω 4 2 ) l k ( − ω 1 2 + ω 3 2 ) b ( − ω 1 2 + ω 2 2 − ω 3 2 + ω 4 2 ) ] \boldsymbol{\tau_{B}}=\begin{bmatrix}\boldsymbol{lk(-\omega_{2}^{2}+\omega_{4}^{2})}\\\boldsymbol{lk(-\omega_{1}^{2}+\omega_{3}^{2})}\\ \boldsymbol{b(-\omega^{2}_{1}+\omega^{2}_{2}-\omega^{2}_{3}+\omega^{2}_{4})}\end{bmatrix} τB= lk(−ω22+ω42)lk(−ω12+ω32)b(−ω12+ω22−ω32+ω42)
牛顿-欧拉方程
-
牛顿方程
牛顿方程是描述刚体在地球坐标系下平动运动的方程,满足牛顿第二定律,其中受到的外力有重力、螺旋桨推力、空气阻力,共同组成飞行器合外力。
定义飞行器位置向量 ξ = [ x y z ] \boldsymbol{\xi}=\left[\begin{array}{l} x \\ y \\ z \end{array}\right] ξ= xyz ,则惯性系下的牛顿方程为:
m ξ ¨ = G + R T B − c ξ ˙ m \ddot{\boldsymbol{\xi}}=\boldsymbol{G}+\boldsymbol{R} \boldsymbol{T}_{B}-c\dot{\boldsymbol{\xi}} mξ¨=G+RTB−cξ˙
其中, c c c是空气阻力系数 -
欧拉方程
欧拉方程是描述机体系转动运动的方程,其中受到的扭矩有螺旋桨产生的扭矩 τ B \boldsymbol{\tau_{B}} τB,陀螺力矩 Γ \boldsymbol{\Gamma} Γ,和离心力矩 ν × ( I ν ) \nu \times(I \nu) ν×(Iν)。
设机体系的角速度向量为 ν = [ p q r ] \boldsymbol{\nu}=\begin{bmatrix}p\\q\\r\end{bmatrix} ν= pqr ,
I ν ˙ + ν × ( I ν ) + Γ = τ B \boldsymbol{I \dot{\nu}+\nu \times(I \nu)+\Gamma=\tau_{B}} Iν˙+ν×(Iν)+Γ=τB
其中, I \boldsymbol{I} I为飞行器的转动张量,表示为:
I = [ I x x 0 0 0 I y y 0 0 0 I z z ] \boldsymbol{I}=\begin{bmatrix}I_{xx} & 0&0\\0&I_{yy}&0\\0&0&I_{zz}\end{bmatrix} I= Ixx000Iyy000Izz
Γ \boldsymbol{\Gamma} Γ是陀螺力矩,其表达式为:
Γ = I r [ q / I x x q / I y y 0 ] ω Γ \boldsymbol{\Gamma}=I_{r}\begin{bmatrix}q/I_{xx}\\q/I_{yy}\\0\end{bmatrix}\omega_{\Gamma} Γ=Ir q/Ixxq/Iyy0 ωΓ
其中, I r I_{r} Ir是螺旋桨的转动惯量, ω Γ = ω 1 − ω 2 + ω 3 − ω 4 \omega_{\Gamma}=\omega_{1}-\omega_{2}+\omega_{3}-\omega_{4} ωΓ=ω1−ω2+ω3−ω4
这里简单解释一下各个力矩。
- 陀螺力矩
这是由于陀螺效应产生的进动力矩,可以根据这些关键词进行进一步的了解,不赘述。- 离心力矩
这是由于质量分布不均产生的离心力矩,可以结合实际生活现象辅助理解,可以搜到相关推导和讲解,这里不赘述。
通常在控制计算时可以忽略这两个力矩,因为四旋翼结构对称,分布均匀,并且四个螺旋桨AB桨叶会抵消陀螺效应,产生的影响也会变得很小。
状态空间方程
基于牛顿欧拉方程,建立四旋翼飞行器的状态空间方程,为后续的控制器设计铺垫。
定义角运动状态向量, X a = [ ϕ θ ψ p q r ] \boldsymbol{X_{a}}=\begin{bmatrix}\phi\\\theta\\\psi \\p\\q\\r\end{bmatrix} Xa= ϕθψpqr ,则状态空间方程为
[ ϕ θ ψ p q r ] ′ = { p + S ϕ T θ q + C ϕ T θ r C ϕ q − S ϕ r S ϕ / C θ q C ϕ / C θ r ( I y y − I z z ) q r / I x x − I r q ω Γ / I x x + τ ϕ / I x x ( I z z − I x x ) p r / I y y + I r p ω Γ / I y y + τ θ / I y y ( I x x − I y y ) / p q / I z z + τ ψ / I z z \begin{bmatrix}\phi\\\theta\\\psi \\p\\q\\r\end{bmatrix}'=\ \left\{\begin{matrix} p+S_{\phi} T_{\theta}q+C_{\phi}T_{\theta}r \\ C_{\phi}q - S_{\phi}r \\ S_{\phi}/C_{\theta}q C_{\phi}/C_{\theta}r \\ (I_{yy}-I_{zz})qr/I_{xx}-I_{r}q\omega_{\Gamma}/I_{xx}+\tau_{\phi}/I_{xx} \\ (I_{zz}-I_{xx})pr/I_{yy}+I_{r}p\omega_{\Gamma}/I_{yy}+\tau_{\theta}/I_{yy}\\ (I_{xx}-I_{yy})/pq/I_{zz}+\tau_{\psi}/I_{zz} \\ \end{matrix}\right. ϕθψpqr ′= ⎩ ⎨ ⎧p+SϕTθq+CϕTθrCϕq−SϕrSϕ/CθqCϕ/Cθr(Iyy−Izz)qr/Ixx−IrqωΓ/Ixx+τϕ/Ixx(Izz−Ixx)pr/Iyy+IrpωΓ/Iyy+τθ/Iyy(Ixx−Iyy)/pq/Izz+τψ/Izz
定义线运动状态向量, X p = [ x y z x ⋅ y ⋅ z ⋅ ] \boldsymbol{X_{p}}=\begin{bmatrix}x\\y\\z \\\overset{\cdot}x\\\overset{\cdot}y\\\overset{\cdot}z\end{bmatrix} Xp= xyzx⋅y⋅z⋅ ,状态空间方程为
[ x y z x ⋅ y ⋅ z ⋅ ] ′ = { x ⋅ y ⋅ z ⋅ ( C ψ S θ C ϕ + S ψ S ϕ ) T / m − c x ˙ ( S ψ S θ C ψ − C ψ S ϕ ) T / m − c y ˙ ( C θ C ϕ ) T / m − g − c z ˙ (1) \begin{bmatrix}x\\y\\z \\\overset{\cdot}x\\\overset{\cdot}y\\\overset{\cdot}z\end{bmatrix}'=\ \left\{\begin{matrix} \overset{\cdot}x \\ \overset{\cdot}y \\ \overset{\cdot}z \\ (C_{\psi}S_{\theta}C_{\phi}+S_{\psi}S_{\phi}) T/m - c\dot{x}\\ (S_{\psi}S_{\theta}C_{\psi}-C_{\psi}S_{\phi}) T/m - c\dot{y}\\ (C_{\theta}C_{\phi}) T/m-g-c\dot{z}\\ \end{matrix}\right. \tag{1} xyzx⋅y⋅z⋅ ′= ⎩ ⎨ ⎧x⋅y⋅z⋅(CψSθCϕ+SψSϕ)T/m−cx˙(SψSθCψ−CψSϕ)T/m−cy˙(CθCϕ)T/m−g−cz˙(1)
总结
-
从状态空间方程可以看出,想要精准的控制四旋翼飞行器的位置和平动运动,需要通过调节飞行器的姿态角度来实现,因此姿态控制就显得尤为重要。
-
本章博客先介绍四旋翼飞行器的建模推导过程,后续将基于本篇博客的模型来开展各类控制算法的实现和仿真,并尽可能做出系统性地分析和讨论。
感谢阅读!




