【大模型LLM面试合集】大语言模型基础_激活函数
1.激活函数
1.激活函数作用
神经网络是线性的,无法解决非线性的问题,加入激活函数就是给模型引入非线性能力;
不同的激活函数,特点和作用不同:
Sigmoid和tanh的特点是将输出限制在(0,1)和(-1,1)之间,说明Sigmoid和tanh适合做概率值的处理,例如LSTM中的各种门;而ReLU就不行,因为ReLU无最大值限制,可能会出现很大值。ReLU适合用于深层网络的训练,而Sigmoid和tanh则不行,因为它们会出现梯度消失。
2.梯度爆炸和梯度消失
模型中的梯度爆炸和梯度消失问题:
- 激活函数导致的梯度消失,像
sigmoid和tanh都会导致梯度消失; - 矩阵连乘也会导致梯度消失,这个原因导致的梯度消失无法通过更换激活函数来避免。直观的说就是在反向传播时,梯度会连乘,当梯度都小于1.0时,就会出现梯度消失;当梯度都大于1.0时,就会出现梯度爆炸。
如何解决梯度爆炸和梯度消失问题:
- 上述第一个问题只需要使用像 ReLU 这种激活函数就可以解决;
- 上述第二个问题没有能够完全解决的方法,目前有一些方法可以很大程度上进行缓解该问题,比如:对梯度做截断解决梯度爆炸问题、残差连接、normalize。由于使用了残差连接和 normalize 之后梯度消失和梯度爆炸已经极少出现了,所以目前可以认为该问题已经解决了。
3.Sigmoid
Sigmoid函数公式:
σ ( z ) = 1 1 + e − z \sigma(z)=\frac{1}{1+e^{-z}} σ(z)=1+e−z1
导数公式:
σ ′ ( z ) = σ ( z ) ( 1 − σ ( z ) ) \sigma^{\prime}(z)=\sigma(z)(1-\sigma(z)) σ′(z)=σ(z)(1−σ(z))
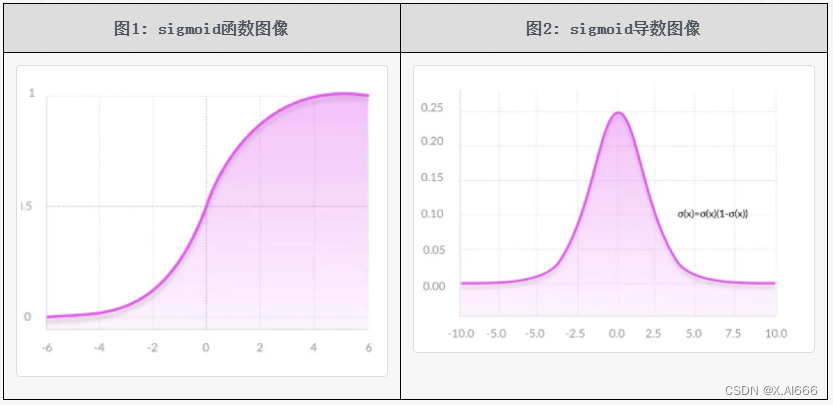
优点:
- 平滑,易于求导;
- 取值范围是
(0, 1),可直接用于求概率值的问题或者分类问题;比如 LSTM 中的门,二分类或者多标签分类问题;
缺点:
- 计算量大,包含幂运算,以及除法运算;
- sigmoid 导数的取值范围是
[0, 0.25],最大值都是小于 1 的,反向传播时又是"链式传导",经过几次相乘之后很容易就会出现梯度消失的问题; - sigmoid 的输出的均值不是0(即zero-centered),这会导致当前层接收到上一层的非0均值的信号作为输入,随着网络的加深,会改变数据的原始分布;
4.Tanh
Tanh的函数公式为:
tanh ( z ) = e z − e − z e z + e − z = 2 1 + e − 2 z − 1 \begin{aligned} \tanh (z) & =\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}} \\ & =\frac{2}{1+e^{-2 z}}-1\end{aligned} tanh(z)=ez+e−zez−e−z=1+e−2z2−1
从上述公式的第二行可以看出,tanh 函数可以由 sigmoid 函数经过平移和拉伸得到。tanh 函数的取值范围是
(-1, 1)。
导数公式
tanh ( x ) ′ = ( e x + e − x ) 2 − ( e x − e − x ) 2 ( e x + e − x ) 2 = 1 − ( tanh ( x ) ) 2 \tanh (x)^{\prime}=\frac{\left(e^{x}+e^{-x}\right)^{2}-\left(e^{x}-e^{-x}\right)^{2}}{\left(e^{x}+e^{-x}\right)^{2}}=1-(\tanh (x))^{2} tanh(x)′=(ex+e−x)2(ex+e−x)2−(ex−e−x)2=1−(tanh(x))2
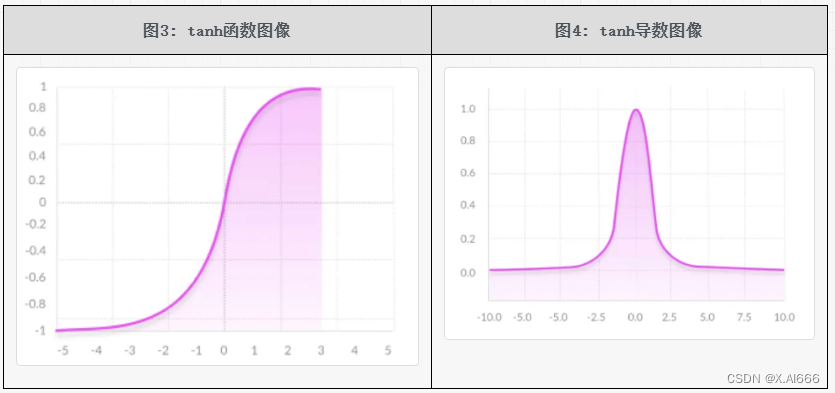
tanh 函数可以理解为是基于 sigmoid 函数的一种改进的激活函数,所以对于 sigmoid 函数的缺点,它能够解决一部分。但是 tanh 函数依然有着不少的缺点。tanh 函数的特点如下:
- 它的输出范围是
(-1, 1),解决了 sigmoid 函数输出的均值不是0(zero-centered)的问题; - tanh 的导数取值范围是
(0, 1),可以看出其在反向传播的"链式传导"过程中的梯度消失问题要比 sigmoid 函数要好一些,但是其依然存在着梯度消失问题; - 幂运算依然存在,计算量比较大;
5.ReLU系列
5.1 ReLU
ReLU 全称为 Rectified Linear Unit,即修正线性单元函数。该函数的公式比较简单,相应的公式和图像如下表所示。
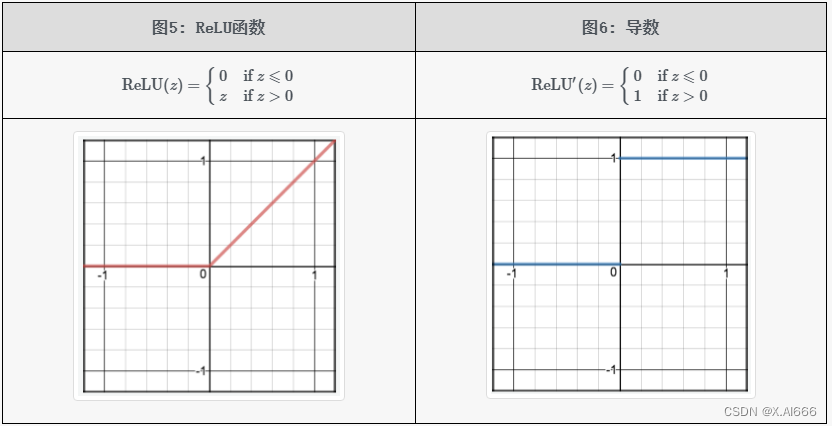
相比于 sigmoid、tanh 这两个激活函数,ReLU 激活函数的优缺点如下:
- 当
z>0时,ReLU 激活函数的导数恒为常数1,这就避免了 sigmoid 和 tanh 会在神经网络层数比较深的时候出现的梯度消失的问题; - 计算复杂度低,不再含有幂运算,只需要一个阈值就能够得到其导数;
- 经过实际实验发现,使用 ReLU 作为激活函数,模型收敛的速度比 sigmoid 和 tanh 快;
- 当
z<0时,ReLU 激活函数的导数恒为常数0,这既带来了一些有利的方面,也导致了一些坏的方面,分别进行描述。- 有利的方面:在深度学习中,目标是从大量数据中学习到关键特征,也就是把密集矩阵转化为稀疏矩阵,保留数据的关键信息,去除噪音,这样的模型就有了鲁棒性。ReLU 激活函数中将
z<0的部分置为0,就是产生稀疏矩阵的过程。 - 坏的方面:将
z<0的部分梯度直接置为0会导致 Dead ReLU Problem(神经元坏死现象)。可能会导致部分神经元不再对输入数据做响应,无论输入什么数据,该部分神经元的参数都不会被更新。(这个问题是一个非常严重的问题,后续不少工作都是在解决这个问题)
- 有利的方面:在深度学习中,目标是从大量数据中学习到关键特征,也就是把密集矩阵转化为稀疏矩阵,保留数据的关键信息,去除噪音,这样的模型就有了鲁棒性。ReLU 激活函数中将
- ReLU 有可能会导致梯度爆炸问题,解决方法是梯度截断;
- ReLU 的输出不是 0 均值的,这个和 sigmoid 类似。(后续的优化工作 ELU 在该问题上解决的比较好,ELU 的输出是近似为0的)
5.2 Leaky ReLU
为了解决 ReLU 的 Dead ReLU 问题,提出了 渗漏整流线性单元(Leaky ReLU),该方法是 ReLU 的一个变体。其在z>0的部分与ReLU一样保持不变;在z<0的部分,采用一个非常小的斜率0.01,其公式如下:
L e a k y ReLU ( z ) = { 0.01 z if z ⩽ 0 z if z > 0 Leaky \operatorname{ReLU}(z)=\left\{\begin{array}{ll}0.01 z & \text { if } z \leqslant 0 \\ z & \text { if } z>0\end{array}\right. LeakyReLU(z)={0.01zz if z⩽0 if z>0
其图像如下所示:
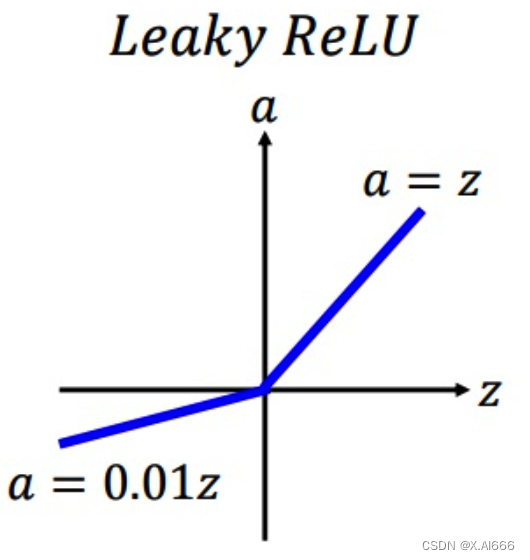
该方法是 ReLU 的一个变体,能够在一定程度上解决 Dead ReLU 问题,但是该方法的缺点是效果并不稳定,所以实际实验中使用该方法的并不多。
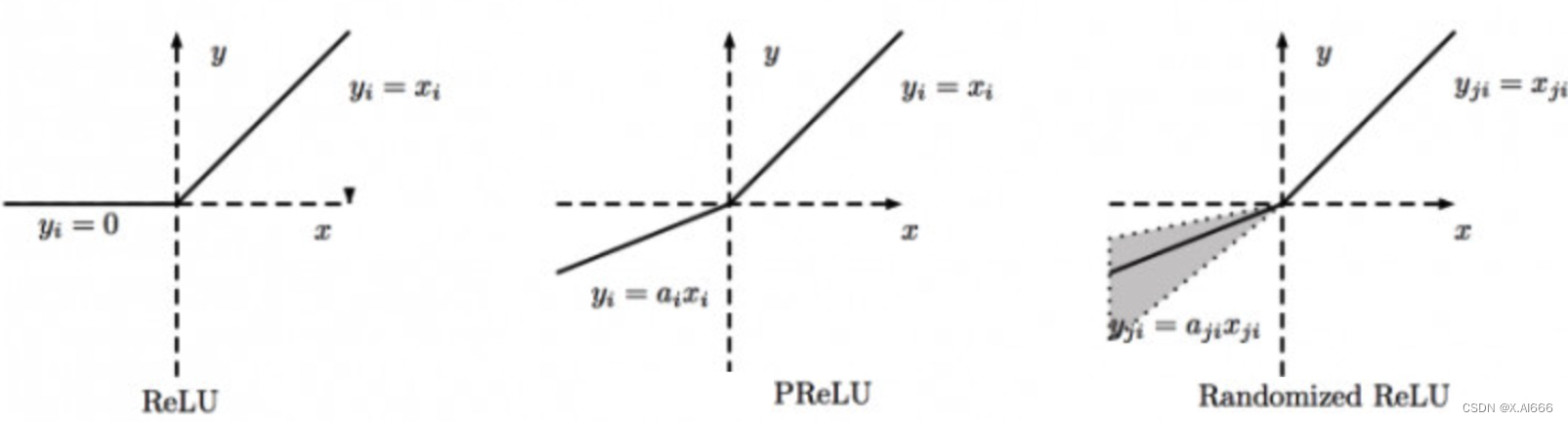
5.3 PReLU, RReLU
PReLU 的全称为 Parametric Relu;PReLU 的全称为 Random ReLU。
这两个方法和 Leaky ReLU 类似,都是 ReLU 的变体。也都是为了解决 Dead ReLU 问题而提出来的。
Leaky ReLU 是在z<0时,设置了一个较小的常数0.01作为斜率。由于这种常数值的斜率并不好,所以 PReLU 提出了可学习的斜率,RReLU 提出了随机的斜率,两者具体的公式如下。
PReLU的公式如下,这里的 α \alpha α是可学习的:
PReLU ( z ) = { α ⋅ z if z ⩽ 0 z if z > 0 \operatorname{PReLU}(z)=\left\{\begin{array}{ll}\alpha \cdot z & \text { if } z \leqslant 0 \\ z & \text { if } z>0\end{array}\right. PReLU(z)={α⋅zz if z⩽0 if z>0
RReLU 的公式如下,这里的 α \alpha α是从一个高斯分布中随机产生的,在训练过程中每次这个 α \alpha α 都是不相同的;在推理时会将这个 α \alpha α都是不相同的;在推理时会将这个
RReLU ( z ) = { α ⋅ z if z ⩽ 0 z if z > 0 \operatorname{RReLU}(z)=\left\{\begin{array}{ll}\alpha \cdot z & \text { if } z \leqslant 0 \\ z & \text { if } z>0\end{array}\right. RReLU(z)={α⋅zz if z⩽0 if z>0
PReLU 和 RReLU 的图像如下所示:
5.4 ELU(指数线性单元)
ELU 的提出也解决了 ReLU 的问题。与 ReLU 相比,ELU 有负值,这会使激活的平均值接近零,让模型学习得更快。
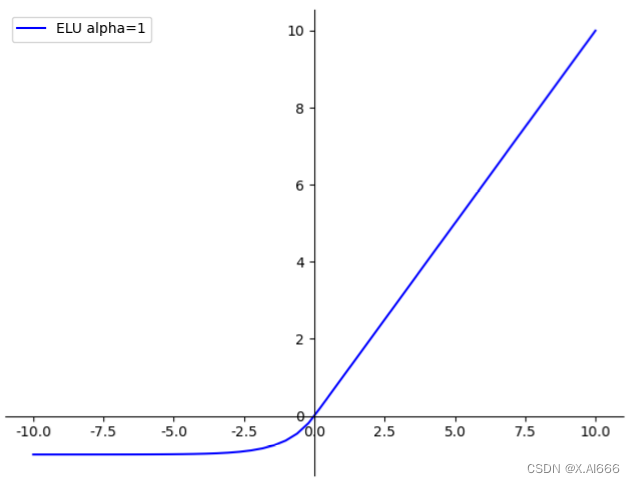
g ( x ) = ELU ( x ) = { x , x > 0 α ( e x − 1 ) , x ⩽ 0 \mathrm{g}(x)=\operatorname{ELU}(x)=\left\{\begin{aligned} x, & x>0 \\ \alpha\left(\mathrm{e}^{x}-1\right), & x \leqslant 0\end{aligned}\right. g(x)=ELU(x)={x,α(ex−1),x>0x⩽0
其中 α \alpha α不是固定的,是通过反向传播学习出来的。ELU的一个小问题是需要exp计算,运算量会更大一些。
- 融合了sigmoid和ReLU,左侧具有软饱和性,右侧无饱和性。
- 右侧线性部分使得ELU能够缓解梯度消失,而左侧软饱能够让ELU对输入变化或噪声更鲁棒。
- ELU的输出均值接近于零,所以收敛速度更快。
6.GeLU
出自2016年的论文《Gaussian Error Linear Units (GELUs)》
先描述一下 GELU 这个激活函数直觉上是基于一个什么思路设计出来的。然后再具体看其如何近似求解、如何代码实现。
6.1 介绍
先看一下 ReLU 激活函数是怎样做的,该函数中包含两种映射:一个是恒等映射(identity mapping),当输入值大于零时就是恒等映射;一个是置零映射(zero mapping),当输入值小于等于零时就是置零映射。
参考 ReLU 激活函数,设计另外一个包含恒等映射和置零映射的激活函数,并且参考 ReLU 函数来看,新激活函数应该有如下性质:
- 在输入
x满足某些条件时,为恒等映射; - 在输入
x满足另外一些条件时,为置零映射; - 在输入
x是一个较大的正值时,更希望为恒等映射;在输入x为一个较小的负值时,更希望是一个置零映射;
以上就是想要新设计的激活函数的性质。
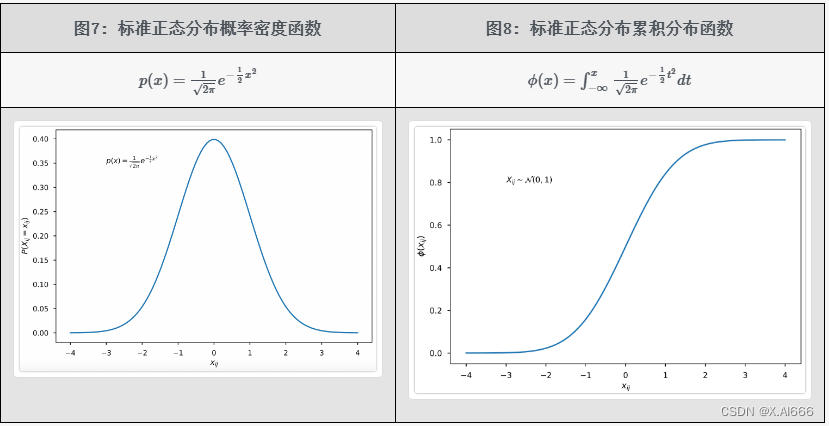
下面的图7和图8是标准正态分布的概率密度函数和累积分布函数的图像。接下来根据下图8中的累积分布函数设计一个新的函数。
符号定义:输入值用 x x x 表示, ϕ ( ⋅ ) ϕ(⋅) ϕ(⋅)表示下图8中的正态分布的累积分布函数, f ( ⋅ ) f(⋅) f(⋅)表示新设计的函数。
设计的新函数:给定输入值 x x x,函数 f ( x ) f(x) f(x)的输出值以 ϕ ( x ) ϕ(x) ϕ(x)的概率采用恒等映射,以 1 − ϕ ( x ) 1−ϕ(x) 1−ϕ(x)的概率采用置零映射。也就是下述公式:
f ( x ) = x ⋅ ϕ ( x ) + 0 ⋅ ( 1 − ϕ ( x ) ) = x ⋅ ϕ ( x ) \begin{aligned} f(x) & =x \cdot \phi(x)+0 \cdot(1-\phi(x)) \\ & =x \cdot \phi(x)\end{aligned} f(x)=x⋅ϕ(x)+0⋅(1−ϕ(x))=x⋅ϕ(x)
然后看一下,新设计的这个公式是否满足上述的激活函数性质。前两条是肯定满足的,主要看一下第3条性质:
- 当输入 x x x 是一个较大的正值时,从图8中可以看出 ϕ ( x ) ϕ(x) ϕ(x)的函数图像逐渐趋近于1,由于函数 f ( x ) f(x) f(x)的输出值以 ϕ ( x ) ϕ(x) ϕ(x)的概率采用恒等映射,所以有接近于1的概率采用恒等映射;
- 当输入 x x x 是一个较小的负值时, ϕ ( x ) ϕ(x) ϕ(x)趋近于0,由于函数 f ( x ) f(x) f(x)以 1 − ϕ ( x ) 1−ϕ(x) 1−ϕ(x)的概率采用置零映射,所以有接近于1的概率采用置零映射;
可以看出新设计的这个函数是满足上述激活函数的性质的。
为了更直观描述设计该函数时的直觉,上述都是采用图8进行描述的,上述公式如果使用图7中的概率密度函数就是如下形式:
f ( x ) = x ⋅ p ( X < x ) + 0 ⋅ ( 1 − p ( X < x ) ) = x ⋅ p ( X < x ) \begin{aligned} f(x) & =x \cdot p(X<x)+0 \cdot(1-p(X<x)) \\ & =x \cdot p(X<x)\end{aligned} f(x)=x⋅p(X<x)+0⋅(1−p(X<x))=x⋅p(X<x)
其中 x x x表示实际的输入值, X X X表示随机变量。到此就得到了GELU的常见形式,公式如下所示:
G E L U = x ⋅ p ( X < x ) = x ⋅ ϕ ( x ) G E L U=x \cdot p(X<x)=x \cdot \phi(x) GELU=x⋅p(X<x)=x⋅ϕ(x)
这里描述的设计 GELU 函数的直觉思路是非常简化的版本,只是为了易于理解。实际在设计这个函数时还需要考虑更多的因素,比如该函数的那几条性质和 ReLU 很像,已经有了 ReLU 为什么还要设计这个函数,这个函数在理论上是否能够解决 ReLU 的存在的 Dead ReLU 等问题;
6.2 函数及导数
GeLU 公式为:
G E L U = x ⋅ ϕ ( x ) G E L U=x \cdot \phi(x) GELU=x⋅ϕ(x)
使用该函数作为激活函数时,需要求解其导数。对其求导可得:
d d x G E L U = ϕ ( x ) + x d d x ϕ ( x ) = ϕ ( x ) + x ⋅ p ( X = x ) \begin{aligned} \frac{d}{d x} G E L U & =\phi(x)+x \frac{d}{d x} \phi(x) \\ & =\phi(x)+x \cdot p(X=x)\end{aligned} dxdGELU=ϕ(x)+xdxdϕ(x)=ϕ(x)+x⋅p(X=x)
其中 X X X是随机变量, p ( X = x ) p(X=x) p(X=x)是图7中的标准正态分布概率密度函数中,随机变量取值为 x x x时的值。
GELU 函数及其导数的图像如下所示。可以看出其函数图像和 ReLU 非常相似,其导数图像也和 ReLU 的导数图像非常相似,不过该图像是连续的。
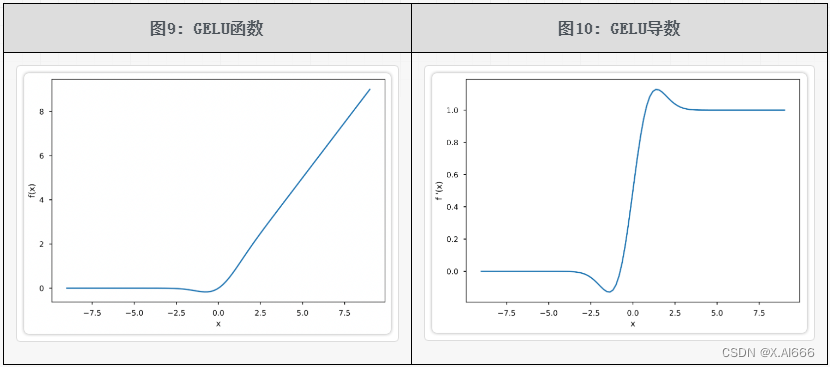
GELU 激活函数的优缺点:
- 从其函数图像可以看出,在负值区域,不再全为0,这解决了 Dead ReLU 问题;
- GELU 函数是处处连续、光滑可导的;
6.3 精确计算
对于 GeLU 的加速计算有两种方法。
第一种方法是精确求解。有一个函数为 Gauss Error function (gef),由于使用率非常高所以在常见的库(比如TensorFlow、PyTorch)中都有针对该函数的优化,该函数的公式如下。
erf ( y ) = 2 π ∫ 0 y e − t 2 d t \operatorname{erf}(y)=\frac{2}{\sqrt{\pi}} \int_{0}^{y} e^{-t^{2}} d t erf(y)=π2∫0ye−t2dt
所以如果能够先求解出 e r f ( ⋅ ) erf(\cdot) erf(⋅),再由该函数求解出 ϕ ( x ) \phi(x) ϕ(x),那么可以加快计算。下面省略具体的推导过程,直接给出计算公式:
ϕ ( x ) = 1 + erf ( x 2 ) 2 \phi(x)=\frac{1+\operatorname{erf}\left(\frac{x}{\sqrt{2}}\right)}{2} ϕ(x)=21+erf(2x)
另一种方法是不精确求解,而是求解其近似值。为了加速计算,还可以使用近似计算的方式。GELU 的近似公式如下所示:
G E L U = 0.5 ∗ x ( 1 + tanh [ 2 π ( x + 0.044715 x 3 ) ] ) G E L U=0.5 * x\left(1+\tanh \left[\sqrt{\frac{2}{\pi}}\left(x+0.044715 x^{3}\right)\right]\right) GELU=0.5∗x(1+tanh[π2(x+0.044715x3)])
7.Swish
出自2017年的论文《Searching for Activation Functions》
该激活函数的公式为:
f ( x ) = x ⋅ σ ( x ) f(x)=x \cdot \sigma(x) f(x)=x⋅σ(x)
Swish导数:
f ′ ( x ) = σ ( x ) + x ⋅ σ ( x ) ⋅ ( 1 − σ ( x ) ) = x ⋅ σ ( x ) + σ ( x ) ( 1 − x ⋅ σ ( x ) ) = f ( x ) + σ ( x ) ⋅ ( 1 − f ( x ) ) \begin{array}{l}f^{\prime}(x) \\ =\sigma(x)+x \cdot \sigma(x) \cdot(1-\sigma(x)) \\ =x \cdot \sigma(x)+\sigma(x)(1-x \cdot \sigma(x)) \\ =f(x)+\sigma(x) \cdot(1-f(x))\end{array} f′(x)=σ(x)+x⋅σ(x)⋅(1−σ(x))=x⋅σ(x)+σ(x)(1−x⋅σ(x))=f(x)+σ(x)⋅(1−f(x))
该激活函数的图像为:
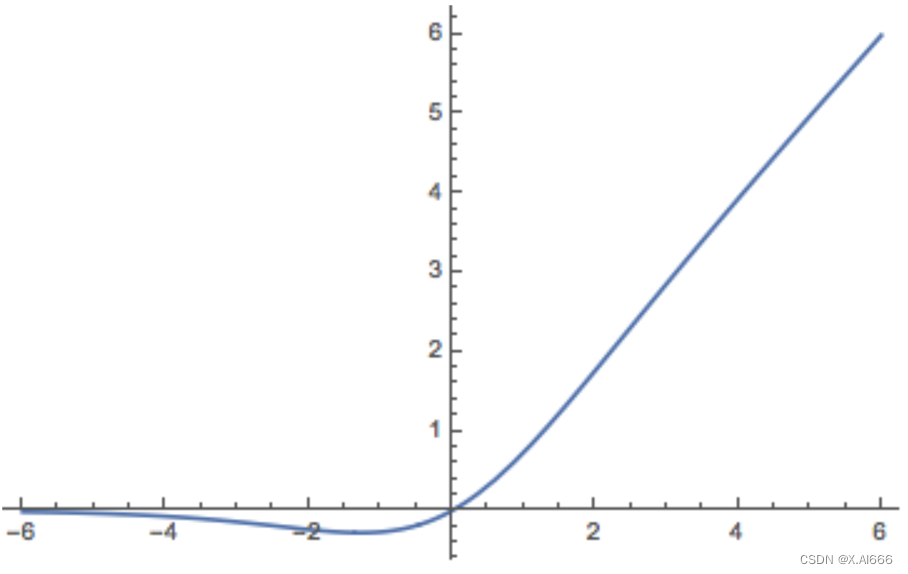
Swish特点:
- 和ReLU一样,没有上边界,因此不会出现梯度饱和现象
- 有下边界,可以产生更强的正则化效果(x左半轴慢慢趋近于0)
- 非单调
- 处处连续且可到,更容易训练
关于正则化效果:x轴越靠近左半轴,纵坐标的值越小,甚至接近于0,如果x值是-10,那么经过激活之后的值接近于0,那么就可以一定程度上过滤掉一部分信息,起到正则化的效果。
8.GLU
PaLM 和 LLaMA 中都使用 SwiGLU 替换了 FFN
出自2017年的论文 Language Modeling with Gated Convolutional Networks
GLU 全称为 Gated Linear Unit,即门控线性单元函数。
参考ReLU激活函数,激活函数GLU的公式为如下公式的形式
GLU ( x ) = x ⊗ σ ( g ( x ) ) \operatorname{GLU}(x)=x \otimes \sigma(g(x)) GLU(x)=x⊗σ(g(x))
这里有一个新符号 g ( x ) g(x) g(x)表示的是向量 x x x经过一层MLP或者卷积, ⊗ ⊗ ⊗表示两个向量逐元素相乘, σ σ σ 表示sigmoid函数。
当 σ ( g ( x ) ) \sigma(g(x)) σ(g(x))趋近于0时表示对 x x x进行阻断,当 σ ( g ( x ) ) \sigma(g(x)) σ(g(x))趋近于1时表示允许 x x x通过,以此实现门控激活函数的效果。
