深度学习基础(Datawhale X 李宏毅苹果书AI夏令营)

深度学习基础(Datawhale X 李宏毅苹果书AI夏令营)

3.1局部极小值和鞍点

3.1.1. 优化失败问题

在神经网络中，当优化到梯度为0的地方，梯度下降就无法继续更新参数了，训练也就停下来了，如图：

梯度为0的情况包含很多种情况：局部最小值、鞍点等。我们统称为临界值。

3.1.2. 判断临界值种类方法

要想知道临界值种类，我们需要知道损失函数的形状。

使用泰勒级数近似来判断：

${\theta }^{\prime }$ 附近的$L(\theta )$可近似为：
$$L(\mathbf{\theta })\approx L\left({\mathbf{\theta }}^{\prime }\right)+{\left(\mathbf{\theta }-{\mathbf{\theta }}^{\prime }\right)}^{\mathrm{T}}\mathbf{g}+\frac{1}{2}{\left(\mathbf{\theta }-{\mathbf{\theta }}^{\prime }\right)}^{\mathrm{T}}\mathbf{H}\left(\mathbf{\theta }-{\mathbf{\theta }}^{\prime }\right).$$
其中，第一项 $L(\theta {)}^{\prime }$ 告诉我们，当 $\theta$ 跟 ${\theta }^{\prime }$ 很近的时候，$L(\theta )$ 应该跟 $L({\theta }^{\prime })$ 还蛮靠近的；第二项 $(\theta -{\theta }^{\prime }{)}^{T}g$ 中，$g$ 代表梯度，它是一个向量，可以弥补 $L({\theta }^{\prime })跟L(\theta )$ 之间的差距。第三项跟梅森矩阵$H$ 有关，

在临界点，梯度$g$ 为0，也就是第二项为0，则损失函数可近似为:
$$L(\mathbf{\theta })\approx L\left({\mathbf{\theta }}^{\prime }\right)+\frac{1}{2}{\left(\mathbf{\theta }-{\mathbf{\theta }}^{\prime }\right)}^{\mathrm{T}}\mathbf{H}\left(\mathbf{\theta }-{\mathbf{\theta }}^{\prime }\right);$$
我们可以根据$\frac{1}{2}{\left(\theta -{\theta }^{\prime }\right)}^{\mathrm{T}}\mathbf{H}\left(\mathbf{\theta }-{\mathbf{\theta }}^{\prime }\right)$来判断在${\mathbf{\theta }}^{\prime }$附近的误差表 (error surface) 到底长什么样子。知道误差表面的“地貌”,我们就可以判断$L({\mathbf{\theta }}^{\prime })$是局部极小值、局部极大值，还是鞍点。为了符号简洁，我们用向量$v$来表示$\theta -{\theta }^{\prime },{\left(\theta -{\theta }^{\prime }\right)}^{\mathrm{T}}H\left(\theta -{\theta }^{\prime }\right)$可改写为$v^{\mathrm{T}}Hv$,

对于三种情况：

1. 如果对所有$v,v^{\mathrm{T}}\mathbf{H}\mathbf{v}>0.$这意味着对任意$\mathbf{\theta },L(\mathbf{\theta })>L({\mathbf{\theta }}^{\prime })$.只要$\mathbf{\theta }$在${\mathbf{\theta }}^{\prime }$附近，$L(\mathbf{\theta })$都大于$L({\mathbf{\theta }}^{\prime })$.这代表$L({\mathbf{\theta }}^{\prime })$是附近的一个最低点，所以它是局部极小值。
2. 如果对所有$v,v^{\mathrm{T}}\mathbf{H}v<0.$这意味着对任意$\mathbf{\theta },L(\mathbf{\theta })<L({\mathbf{\theta }}^{\prime }),{\mathbf{\theta }}^{\prime }$是附近最高的一个点，$L({\mathbf{\theta }}^{\prime })$是局部极大值。
3. 如果对于$v$，$v^{\mathrm{T}}Hv$有时候大于零，有时候小于零。这意味着在${\theta }^{\prime }$附近，有时候$L(\mathbf{\theta })>L({\mathbf{\theta }}^{\prime })$,有时候$L(\mathbf{\theta })<L({\mathbf{\theta }}^{\prime })$.因此在.${\mathbf{\theta }}^{\prime }$附近，$L({\mathbf{\theta }}^{\prime })$既不是局部极大值，也不是局部极小值，而是鞍点。

一个更简单的计算方法：只看$H$的特征值：

若$H$的所有特征值都是正的，$H$为正定矩阵，则$v^{\mathrm{T}}Hv>0$,临界点是局部极小值。若$H$的所有特征值都是负的，$\mathbf{H}$为负定矩阵，则${\mathbf{v}}^{\mathrm{T}}\mathbf{H}\mathbf{v}<0$,临界点是局部极大值。若$H$的特征值有正有负，临界点是鞍点。

3.2 批量和动量

3.2.1 批量大小对梯度下降法的影响

1. 批量梯度下降(BGD)

   使用整个训练集的优化算法被称为批量(batch)或确定性(deterministic)梯度算法，因为它们会在一个大批量中同时处理所有样本。

2. 随机梯度下降（SGD)

   随机梯度下降法不同于批量梯度下降，随机梯度下降是在每次迭代时使用一个样本来对参数进行更新（mini-batch size =1）。

• BGD每次更新更稳定，更准确；SGD在梯度上引入随机噪声，在非凸优化问题种，更容易逃离局部最小值，优化效果更好。

• BGD遇到临界值，梯度为0的点时，难以逃离；而SGD容易逃出局部极小点等。

• BGD泛化性一般情况下比SGD差。

3.2.2 动量法

动量法（momentum method）是一个可以对抗鞍点或局部最小值的方法。即在梯度为0的点时，可以利用自身的动量在一定情况下冲出局部极小值和鞍点等。

与传统的梯度下降不一样，动量法引入动量后，每次在移动参数的时候，不是只往梯度的反方向来移动参数，而是根据梯度的反方向加上前一步移动的方向决定移动方向。

这样让梯度下降在梯度为0的点时有一定可能继续继续更新。

3 自适应学习率

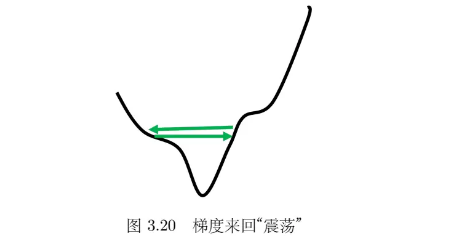
临界点其实不一定是在训练一个网络的时候会遇到的最大的障碍。随着迭代次数增多，虽然损失不再下降，但是梯度的范数并没有真的变得很小。学习率过大，在陡峭的地方，梯度会在临界点附近震荡；学习率过低，到达平缓的地方训练速度会变慢。

最原始的梯度下降连简单的误差表面都做不好，因此需要更好的梯度下降的版本。在梯度下降里面，所有的参数都是设同样的学习率，这显然是不够的，应该要为每一个参数定制化学习率，即引入自适应学习率（adaptive learning rate）的方法，给每一个参数不同的学习率。

如果在某一个方向上，梯度的值很小，非常平坦，我们会希望学习率调大一点；如果在某一个方向上非常陡峭，坡度很大，我们会希望学习率可以设得小一点。

3.1 AdaGrad

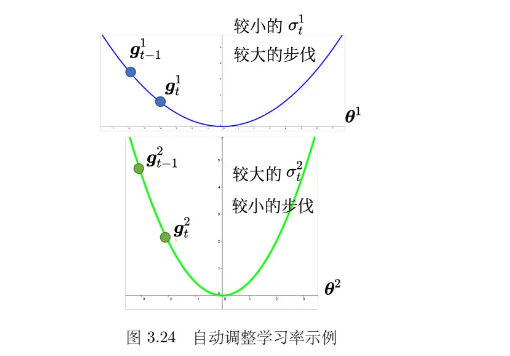
AdaGrad（Adaptive Gradient） 是典型的自适应学习率方法，可以做到梯度比较大的时候，学习率就减小，梯度比较小的时候，学习率就放大。随着梯度的不同，每一个参数的梯度的不同，可以自动调整学习率的大小。

学习率从$\eta 改成\frac{\eta }{{\sigma }_t^i}$的时候, 学习率就变得参数相关（parameter dependent），一个常见方法是对于每一维，把原来学习率 η 除以之前所有梯度在该维的的均方根 。更新过程如下:
$${\mathbf{\theta }}_{n+1}^i={\mathbf{\theta }}_n^i-\frac{\eta }{{\sigma }_n^i}{\mathbf{g}}_n^i$$
其中${\theta }_n^i$是初始化参数。而${\sigma }_n^i$的计算过程为
$${\sigma }_n^i=\sqrt{\frac{1}{n+1}\sum _{j=0}^n({\mathbf{g}}_j^i{)}^2}=\sqrt{\frac{n}{n+1}({\sigma }_{n-1}^i{)}^2+\frac{1}{n+1}({\mathbf{g}}_n^i{)}^2}$$

缺陷：一开始的梯度可能会对后面的结果造成较大影响，在非凸性优化中收敛较慢。

3.2 RMSProp

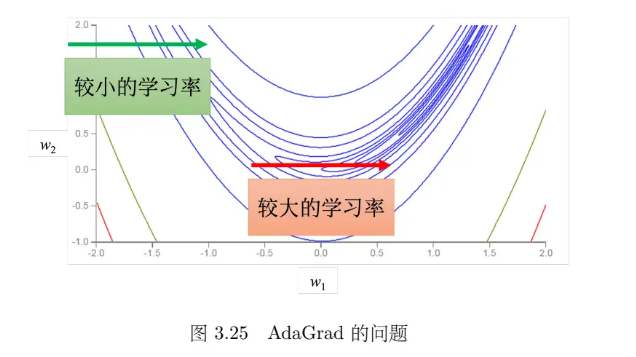
同一个参数需要的学习率，也会随着时间而改变。在图 3.25 中的误差表面中，如果考虑横轴方向，绿色箭头处坡度比较陡峭，需要较小的学习率，但是走到红色箭头处，坡度变得平坦了起来，需要较大的学习率。同一个参数的同个方向，学习率也需要动态调整（AdaGrad的变化较缓慢）。RMSprop（Root Mean Squared propagation） 可以更好的解决。

它其他地方和AdaGrad一样，只是将 ${\theta }_n^i$替换为指数加权均方根：
$${\sigma }_n^i=\sqrt{\alpha ({\sigma }_{n-1}^i{)}^2+(1-\alpha )(g_n^i{)}^2}=\sqrt{{\alpha }^t(g_0^i{)}^2+(1-\alpha )\sum _{j=1}^n{\alpha }^{t-j}(g_j^j{)}^2}$$

其中 0<α<10<α<1，其是一个可以调整的超参数。在 AdaGrad 算均方根的时候，每一个梯度都有同等的重要性，但在 RMSprop 里面，可以自己调整现在的这个梯度的重要性。如果 αα 设很小趋近于 00，代表当前的梯度相较于之前算出来的梯度而言更重要；反之亦然。RMSProp 可以使得梯度的变化更受当前梯度影响，变化更灵活。

3.3 Adam

最常用的优化的策略或者 优化器（optimizer） 是 Adam（Adaptive moment estimation）。Adam 可以看作 RMSprop 加上 动量，其使用动量作为参数更新方向，并且能够自适应调整学习率。PyTorch 内置 Adam 优化器。

4. 学习率调度

对于在误差表面训练不起来的情况，加上 AdaGrad 这样的自适应学习率后，在梯度很小的方向，学习率会自动变大，步伐就可以变大，从而不断前进。但是梯度分量小的方向上可能因为梯度的累积导致学习率增大，进而导致震荡。

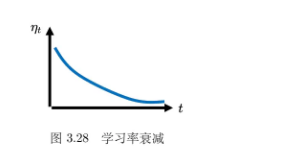
通过 学习率调度（learning rate scheduling） 可以解决这个问题。即把之前固定的$\eta$ 修改为随时间变换。学习率调度中最常见的策略是 学习率衰减（learning rate decay），也称为 学习率退火（learning rateannealing）。它使得随着参数的不断更新，让 η越来越小，使得后期变化更平缓。
$${\theta }_{t+1}^i\leftarrow {\theta }_t^i-\frac{{\eta }_t}{{\sigma }_t^i}{\mathbf{g}}_t^i$$

除了学习率下降以外，还有另外一个经典的学习率调度的方式———预热。预热的方法是让学习率先变大后变小，至于变到多大、变大的速度、变小的速度是超参数。一开始学习率比较小是用来探索收集一些有关误差表面的情报，先收集有关 σσ 的统计数据，等 σσ 统计得比较精准以后，再让学习率慢慢爬升。Adam 的进阶版———RAdam 运用了相关策略。

5. 优化总结

从原始的梯度下降进化到最后：
$${\mathbf{\theta }}_{t+1}^i={\mathbf{\theta }}_t^i-\frac{{\eta }_t}{{\sigma }_t^i}{\mathbf{m}}_t^i$$
其中$m_t$是动量。这个是目前优化的完整的版本，这种优化器除了 Adam 以外，还有各种变形。但其实各种变形是使用不同的方式
来计算${\mathbf{m}}_t^i$或${\sigma }_t^i$,或者是使用不同的学习率调度的方式。

6. 分类

6.1 分类与回归的关系

回归是输入一个向量$\mathbf{x}$,输出$\hat{y}$,我们希望$\hat{y}$跟某一个标签$y$越接近越好，$y$是要学习的目标。而分类可当作回归来看，输入$x$后，输出仍然是一个标量$\hat{y}$,要让它跟正确答案的那个类越接近越好。$\hat{y}$是一个数字，我们可以把类也变成数字。

6.2 带有 softmax 的分类

实际做分类的时候，往往会把$\hat{y}$通过 softmax 函数 得到$y^{\prime }$,再去计算$y^{\prime }$跟$y$之间的距离(损失)。
softmax 的计算如下：
$$y_i^{\prime }=\frac{\exp ({\hat{y}}_i)}{{\sum }_j\exp ({\hat{y}}_j)}$$
softmax 除了归一化，让$\hat{y}$的每一维变成0到 1 之间，和为1以外，它还会让大的值跟小的值的差距更大。这样才能更好地跟标签的计算相似度。

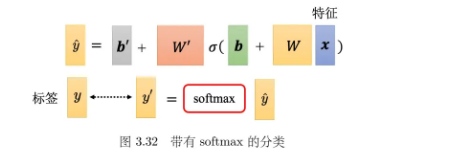
6.3 分类损失

综上，我们把$x$输入到一个网络里面产生$\hat{y}$后，通过 softmax 得到$y^{\prime }$,再去计算$y^{\prime }$跟$y_i$之间的距离 e。
可以用均方误差定义损失：
$$e=\sum _i(y_i^{\prime }-y_i{)}^2$$
分类中更常用交叉熵：
$$e=-\sum y_i\ln y_i^{\prime }$$
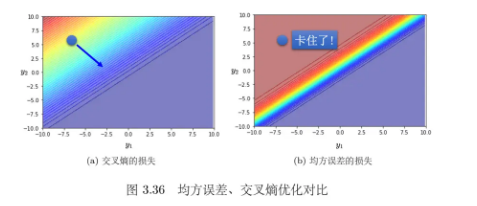
考虑两个参数的情形。假设参数优化开始的时候，对应的损失都是左上角。如果选择交叉熵，左上角圆圈所在的点有斜率的，所以可以通过梯度，一路往右下的地方“走”；如果选均方误差，如图 3.36(b) 所示，左上角圆圈就卡住了，均方误差在这种损失很大的地方，它是非常平坦的，其梯度是非常小趋近于 0 的。（由softmax的性质决定）因此做分类时，选均方误差的时候，如果没有好的优化器，有非常大的可能性会训练不起来。

7. 实践：HW3(CNN)卷积神经网络-图像分类

神经网络任务流程

1. 导入所需要的库

   # 导入必要的库
   import numpy as np
   import pandas as pd
   import torch
   import os
   import torch.nn as nn
   import torchvision.transforms as transforms
   from PIL import Image
   # “ConcatDataset” 和 “Subset” 在进行半监督学习时可能是有用的。
   from torch.utils.data import ConcatDataset, DataLoader, Subset, Dataset
   from torchvision.datasets import DatasetFolder, VisionDataset
   # 这个是用来显示进度条的。
   from tqdm.auto import tqdm
   import random
   

2. 数据准备和预处理

3. 定义网络模型

4. 定义损失函数和优化器等

5. 训练模型

6. 评估模型

7. 进行预测

我们可以继续使用等方法继续对前面的模型进行优化，不过现在还没有完成，待续，基础代码皆实现在github仓库中。