宏定义判定x是否为整数_整数与整数都还差不多从“高斯整数”到“代数整数”...

大家好，我是大老李。这期节目灵感来自于之前有关超越数节目的听众留言。

之前节目有一位署名为“豆角mm”的听众说：“那虚数也有超越数吧，然后复数大部分就是超越复数了”。我一想还真有点道理，因为有些复数是代数方程的根，有些不是，所以自然地就把复数中分出一个“代数复数”和“超越复数”。但是那样区分有没有什么实用价值就有待各位自己发掘了。

此处有个小插曲：之前节目中，我一直认为代数数是实数中的一个子集，但是有听众指出，代数数里有复数。维基百科上代数数的定义是：

代数数是代数与数论中的重要概念，指任何整系数多项式的复根。

确实包含虚数。但是超越数的定义是：

在数论中，超越数(transcendental number)是指任何一个不是代数数的无理数。

这样看，超越数又不包含虚数。如此一来，那么“超越复数”和“代数实数”的概念到底有吗？不管怎样，请大家注意以上两者的定义。

有另一位署名 “ali2233”的听众留言说“请大老李聊一下“高斯整数”。我一听，这个话题还与前面听众的留言有关。代数数有点像在实数里挖出的一个坑，这个坑比实数小，但比有理数大。而“高斯整数”就是数学家在复数集合中挖的一个坑，这个坑比复数小但是比整数大，它是按照”整数“的挖法挖出来的。这集我们就来聊聊”高斯整数”。

首先我们要考虑的一个问题是“为什么”要有“高斯整数”？各位要记住数学家引入一个新的概念，定义，必然是有原因的，所以我们要问下“为什么要有...”？高斯整数的引入还是可以从一个质因数分解的问题开始考虑。

比如对整数5，当然是质数。而当我们把数系扩展到复数范围内之后，有人发现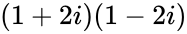等于5。这下有意思了？这个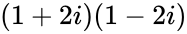算不算对5的因式分解呢？

你可能会先问：考虑这样的问题有意义吗？但数学里很多东西一开始就是从貌似无意义的一些思考开始的。如果你一开始就觉得它无意义，那么你就错过了很多发现的可能。我们先不管，先继续考虑这个因数分解。

我们需要解决的第一个问题就是：在什么样的范围内分解？不确定范围的话，分解过程可以是无止境的。所以我们就需要在复数范围中找出类似于“整数”的东西。

那整数有什么特性呢？我们第一感能想到的就是整数加减另一个整数，还是整数。整数乘以整数，还是整数，但是整数除以整数，就可能不是整数了 。也许最后一个特性才是整数最重要的特性，因为正是因为整数除以整数不一定是整数了，整数不够用了，我们才引入了分数。另外减法本质上是加另一个数的相反数，所以可以本质上还是一种加法。那么以上整数的性质，我们就可以说整数对加法和乘法是“封闭”的，但是对乘法的逆运算，除法不封闭。“封闭”的意思，就是结果仍然在原始预算的集合内。

“闭包的定义” (转自维基百科 )：数学中，若对某个集合的成员进行一种运算，生成的仍然是这个集合的成员，则该集合被称为在这个运算下闭合。例如，实数在减法下闭合，但自然数不行：自然数 3 和 7 的减法 3 − 7 的结果不是自然数。

类似的，一个集合被称为在某些运算的搜集下闭合，如果它在每个运算之下都闭合。

一个集合在某个运算或某些运算的搜集下闭合被称为满足闭包性质。闭包性质经常作为公理，通常叫做闭包公理。现代集合论通常这样定义：运算为在集合间的映射。所以向一个结构增加闭包性质作为公理是多余的，尽管它对于子集是否闭合的问题仍有意义。

那么就请听众思考下，复数范围内，怎么可以找出一个子集，使得其中的元素加法和乘法仍然是封闭的，但是除法不封闭。相信你都不用过多思考，你马上能想到这样一个复数的子集，就是a+bi类型的数，其中a和b都是整数。如果你能想到这种数，那么恭喜你，你也发现了“高斯整数”！

高斯整数就是复平面上的整数格点：

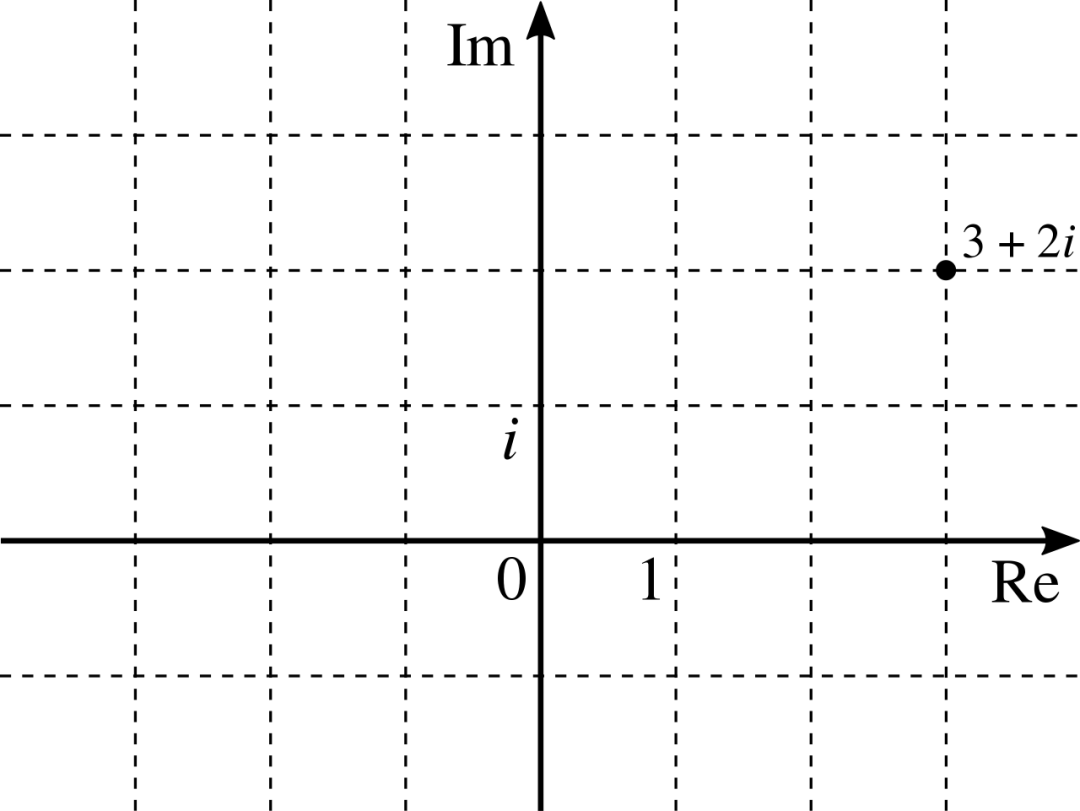
先别高兴太早，我们稍微分析一下“高斯整数”的性质：首先a+bi这种数，如果a和b都是整数，那么显然两个这种数相加相乘，其结果还是能写成a+bi形式，其中a、b仍然是整数，所以它对加法和乘法具有封闭性。对除法，它就不一定封闭了。比如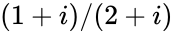结果就无法写成高斯整数形式了，这一点请各位自行验证。

所以结果太好了，我们发现高斯整数对加法，乘法封闭，对除法不封闭。那么它就有了成为一种“整数”的良好潜质。而且它还符合原先整数运算的一些特性，比如交换律，结合律，分配率，等等，这都使它更像整数。

但在我们考虑如何在这种整数范围内做质因数分解之前，我们还要做一些小小的规定。因为所有的高斯整数除以+-1，+-i，都能除尽，所以我们把+-1，+-i既不算做质数，也不算做合数。这也是很自然的，类似于整数里，我们不把1当质数的。

但要注意，这样规定有个小小的缺点是，看似两种不同的高斯整数分解结果，如果其中一个结果可以通过乘若干个+-1和+-i，转换为另一个，那么我们就认为这两种结果本质上是同一种，这是大家要注意的。

高斯整数的质因数分解例子：

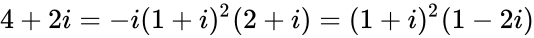
以上两种分解形式视为同一种。

那现在就可以考虑高斯整数中，是什么样的数算质数？它的定义当然很自然：如果一个高斯整数的因子只有自身或者+-1，+-i，则它就是高斯质数。

那么如何判定一个高斯整数是否是高斯质数？这是一个很有意思的问题。比如我们可以考察下，通常的质数是不是高斯质数？你会发现2可以分解成(1+i)(1-i)，但是3就感觉不能再分解了。而5又可以分解成(1+2i)(1-2i)，所以我们发现原先整数中的一些质数是高斯质数，有些不是。

还好数学家已经帮我们找出了一个高斯质数的判定定理，分两种情况：

如果高斯整数中的a,或b有一个是0，即，这个数是实数或者纯虚数时，当且仅当a或b是4n+3形的质数(也就是除以4要余3的质数)时，它是高斯质数。比如7除以4余3，所以7或者7i都是高斯质数。

但5除以4余1，所以5或5i就不是高斯质数。5前面说了，可以分解成(1+2i)(1-2i)，而5i，能分解成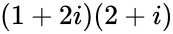 。(有时也可以把5i的分解写作：。这里要注意一下，i虽然本身不是质数或者合数，但有时也它出现在分解结果里。把i乘如某个其他因子就可以避免i出现，这个问题无伤大雅。)

如果a,b都不为0， 则当且仅当是质数时，a+bi是高斯质数。以上这个判定定理的证明不算复杂，请各位自行查阅了。而且它很好用， 很方便做质因数分解时判定是否分解到最小了。

好了，高斯质数的定义和判定方法也有了。下一步可以考虑的第一个问题就是“唯一因子分解定理”是否还成立呢？我们知道在整数范围内，一个整数的质因数分解只有一种结果，这个结论叫“整数的唯一因子分解定理”，又叫“算术基本定理”，可见其重要性。

算术基本定理定义(转自维基百科)：

算术基本定理，又称为正整数的唯一分解定理，即：每个大于1的自然数，要么本身就是质数，要么可以写为2个或以上的质数的积，而且这些质因子按大小排列之后，写法仅有一种方式。

算术基本定理的内容由两部分构成：

分解的存在性：
分解的唯一性，即若不考虑排列的顺序，正整数分解为素数乘积的方式是唯一的。

算术基本定理是初等数论中一个基本的定理，也是许多其他定理的逻辑支撑点和出发点。

高斯证明了高斯整数也是具有唯一因子分解定理的，这是一个很好的性质。稍后我们会看到在其他一些“整数”类型中，唯一因子分解定理不成立。

那无论如何，我们得到了一种新的整数，“高斯整数”，这是一个新大陆，很多整数中的命题和猜想几乎都可以平移到这个块新大陆上考察。

比如，高斯整数里有(非平凡的)勾股数组吗？就是让，a,b,c都是高斯整数。结果当然有，比如：

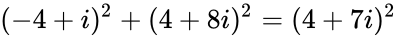
请你考虑一下有没有参数化生成公式。

接下来你马上想到费马大定理的对高斯整数会如何？费马大定理说对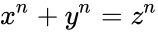这样的方程，当n>=3时，方程无整数解，但有没有高斯整数范围内的解呢？目前猜想是无解，这个问题仍是开放问题，有人悬赏500美元，任何人能给出一个反例即得，想赚外快的朋友赶紧行动。

还有一个类似的问题叫Beal猜想是说对这种类型的方程这样类型的方程，如果三个指数x,y,z都大于2，且这个方程有整数解，则a,b,c必有质数公因子，也就是a,b,c不互质。这个猜想在整数范围内非常难，因为美国数学会(AMS)目前对此猜想的悬赏达到了1百万美元。

美国数学会关于Beal猜想的悬赏专页：

有意思的是这个猜想在高斯整数范围内，找到了一个反例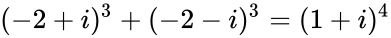：，但是目前仅找到这样一个反例。有人悬赏50美元，给任何人找到一个新的反例。个人感觉这个悬赏比之前的费马大定理的反例应该容易多了。

再聊一个“完美数”问题：一个整数是完美数，当且仅当其全部因子之和，包括1，但不包含自身。这个和是其本身。比如6的因子有1，2，3，而1+2+3=6，所以6是一个完美数。那高斯整数中有没有完美数呢？目前还没有人找到。有一个很接近的例子是。它的所有因子之和是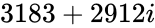。此问题悬赏金额为100美元

完美数定义(转自维基百科)：

完全数，又称完美数或完备数，是一些特殊的自然数：它所有的真因子(即除了自身以外的约数)的和，恰好等于它本身，完全数不可能是楔形数、平方数、佩尔数或费波那契数。

例如：第一个完全数是6，它有约数1、2、3、6，除去它本身6外，其余3个数相加，1+2+3＝6，恰好等于本身。第二个完全数是28，它有约数1、2、4、7、14、28，除去它本身28外，其余5个数相加，1+2+4+7+14＝28，也恰好等于本身。后面的数是496、8128。

好了，以上只是简单聊了三个有关在整数范围内的命题，推广到高斯整数范围的情况。其实有关整数的命题和猜想太多了，什么：哥德巴赫猜想，素数定理，亲和数，婚约数，完美立方体数，梅森素数，华林问题等等。其中每一个扩展到高斯整数范围内又都是一个非常大的话题，这里就不一一列举了。

到这里，对高斯整数大家应该有所了解了，但是复数范围内，定义新的“整数”只有高斯整数这一种方法吗？显然不是。比如代数整数就是另一种。代数整数与不久前介绍的代数数很相关。代数数的定义是：它是一个多项式方程的根。但是代数整数要求再更严格一点，要求这个多项式是整数系数多项式，且次数最高的项的的系数必须是1，称为“首一多项式“，意思是“第一项系数为1”。

代数整数定义(转自维基百科)：

在数学里，代数整数(algebraic integer)是复数中的一类。一个复数α是代数整数当且仅当它是某个个整系数的首一多项式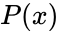的根。其中首一(英文：monic)意谓最高幂次项的系数是1。

因此，所有代数整数都是代数数，但并非所有代数数都是代数整数。所有代数整数构成一个环，通常记作 。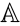

你能很容易的验证代数整数对加法和乘法有封闭性，但是对除法不封闭，其实这两条性质就是一个数字可以被称为”整数“的基本条件。一旦定义好了代数整数，我们又可以在代数整数中考虑什么是代数质数、唯一因子分解定理、费马大定理、完美数、哥德巴赫猜想等等的问题了。

那还有其他定义整数的方法吗？还有，而且很简单。比如对高斯整数中，如果我们把i看作的话，那换做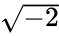也可以啊，即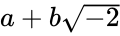这种类型的数，也能构成一套整数啊。因为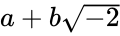类型的数也满足加法、乘法封闭，除法不封闭。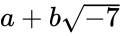，等等都可以。换成正数也可以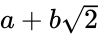，类型的数也能构成一套整数，等等。

这样你会发现，我们一下子有了无穷多套“整数”，这里面可以研究的问题一下子爆发了。就最基本的唯一因子分解情况，高斯发现，有些类型的整数里能保持，有些则不能保持唯一因子分解定理。高斯猜想，如果根号里是负数的话，只有1, 2, 3, 7, 11, 19, 43, 67, 163这9个数能保持唯一因子分解的性质，这个猜想在1952年，被电气工程师黑格纳证明，所以这9个数被称为“黑格纳”数。想具体了解的，请听我之前一期节目叫“有意思的163，有关黑格纳数”的节目。

而高斯的这一大类猜想：被称为“虚二次域上的高斯类数”问题，其中未解的命题还非常多，这里我无法展开了。

总结这期节目，我想说的是，数学家很会“来事”，“整数”这么基本的概念他们也能推而广之。要点就是抓住要有两个运算，其中一个运算和逆运算都保持封闭，另一个运算也封闭，但逆运算比封闭，那么你就有发明一种整数的良好基础，然后整数的一堆性质和猜想就可以套用上去开始考察。

而且可以告诉大家发明高斯整数，代数整数等等并不是为了好玩，它们还都是很用的。比如高斯就是在研究数论中非常重要的二次互反律过程中，发明高斯整数概念的。而后来，人们又把各种 整数的形状进一步抽象，总结出了“环”和”域“这些代数结果，这些以后有机会再讲。

最后给大家留一个思考题 ，我请大家考虑下从矩阵能否定义“矩阵整数”？因为矩阵也有加法和乘法，所以它就有成为整数的很好“潜质”？虽然矩阵的乘法没有交换律，但又有谁规定整数必须符合乘法交换律呢？所以我觉得这不是障碍。而一旦你定义好了“矩阵整数”，你就可以考察一下有没有矩阵质数，有没有唯一因子分解定理，有没有勾股数组等等问题，相信会非常有意思的。

当然，你也可以完全不用矩阵，用其他对象，只要有两种运算就是好的开始。如果你有好的发现，我也很欢迎你发给我看看，分享你的成果。

如果你喜欢大老李的文章，请记得点赞，分享和订阅。

参阅：有意思的163–黑格纳数 (音频讲稿)

喜马拉雅：https://www.ximalaya.com/keji/6310606/

微信关注：dalaoli_shuxue

B站: https://space.bilibili.com/423722633

知乎：https://zhuanlan.zhihu.com/dalaoli-shuxue/

电邮：dalaoliliaoshuxue@gmail.com

参考链接：http://www.mathpuzzle.com/Gaussians.html

http://mathworld.wolfram.com/GaussianInteger.html

https://zh.wikipedia.org/wiki/%E9%AB%98%E6%96%AF%E6%95%B4%E6%95%B8

https://en.wikipedia.org/wiki/Table_of_Gaussian_integer_factorizations

https://www.alpertron.com.ar/GAUSSIAN.HTM

https://brilliant.org/wiki/gaussian-integers/