用自底向上算法为一组整数构造一个大根堆。_Mathematical Cryptography笔记：整数分解和RSA...

3.1 Euler’s Formula and Roots Modulo pq

Euler’s Formula for

:

和

为两个不相等的质数，令

,

,

(mod

)

In particular： 若 p 和 q 为奇质数

,

,

(mod pq）

Prove：

• 根据假设可知，
  且
• 计算
  (
  为整数)
  
  ​
  (mod
  ) (费马小定理)
  
  ​
  (mod
  )
• 同理可证
  (mod q)
• 综上该定理得证

Remark：个人感觉教材这里不是很清楚，可以看出只要 g 同时是 p-1, q-1 的因素证明同样也成立 ，所以定理中 g 未必需要是最大公因数，是公因数就行了。否则 gcd 只有一个，定理里又有 “in particular” 看起来就感到矛盾。

Proposition1：

是质数，令

是一个满足

的整数. 显然

有一个关于 modulo

的 inverse，记作

(mod

). 则

(mod

) 有唯一解

(mod

).

Prove：

• 若
  ，则
  是唯一解，齐活，故 generally，假设
  (mod
  )
• (mod
  ）即存在整数
  ，
  ，易验证
  是其一个解

(mod p)

​

(mod

)

​

(mod

)

​

(mod

)

​

(mod

)

• 再证唯一性，假设
  均为解，根据上一条，有
  (mod
  )

Remark：如果前提

被省略，则

(mod

) 对某些

有解，即解未必存在，即便存在解，解会存在多个

推广：对于模数不再是质数

的情况下相似，If we know how to factor

Proposition2：

为两个不相等的质数，令

是一个满足

的整数，显然

有一个关于 modulo

的 inverse，记作

(mod

). 则

(mod

) 有唯一解

(mod

)

Prove：类似Proposition1的证明，但将费马小定理改为 Euler's formula，只考虑

的情况，else omitted

• (mod
  )
  存在整数
  ,
• 验证
  是
  (mod
  ) 的一个解
  (mod
  )
  (mod
  )
  (mod
  )
  (mod
  )
  (mod
  )
• 证明 uniqueness ，假设
  是一个解
  (mod
  )
  (mod
  )
  (mod
  )
  (mod
  )
  
  （第一个
  因为
  ，第三个
  因为开头的欧拉公式）
  
  since
  是一个解 所以
  (mod
  ) 的每个解都等于
  (mod
  ) ，故唯一性

Remark1：该定理提供一种求解

(mod

) 的算法，即先计算

(mod

) 中的 inverse

，再计算

mod pq

Remark2：通常可以用减小

的方式加快运算速度。

，求解

(mod

) ，根据欧拉公式

(mod

) ，记

，

(mod

) ，故使用这个 smaller value of

，

mod

依旧是

(mod

) 的一个解

• 虽然
  的值求出来可大可小能变，但取了 modulo 后是 unique 的

背景：RSA公钥密码系统基于 the difficulty of solving equations of the form

(mod

) 其中

均已知，

it is difficult to take e-th roots modulo N

同时也可以看出为什么大质数分解对解答上面的问题很 crucial

3.2 The RSA Public Key Cryptosystem

加密过程如下图：

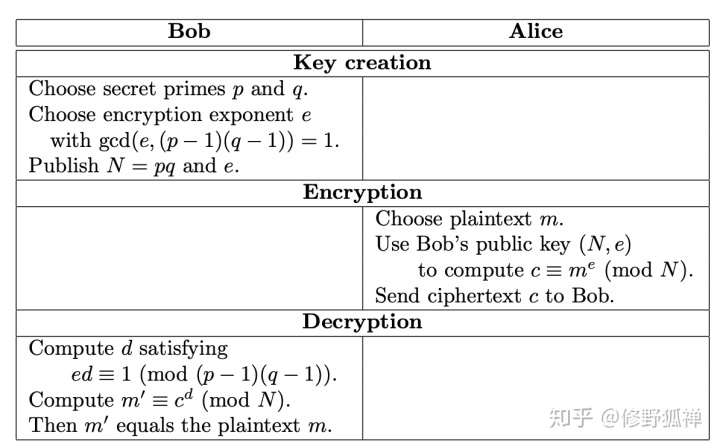
N​ 被称为 modulus，e​ 被称为 encryption exponent，d​ 被称为 decryption exponent

为什么 RSA 是安全的

• set up：
  为大质数，令
  ，
  为整数
• Problem：求解
  (mod
  )
• Easy：Bob 知道
  的值，故能轻松求解（参见上一节 Proposition 2）
• Hard：Eve不知道
  的值，故不能轻易求解
• Dichotomy： Solving
  (mod
  ) 对一些知道某个 trapdoor information 的人易解，但对其他所有人难解

Remark1：如果

比较小则加密比较 efficient；如果

比较小则解密比较 efficient。值得注意的是

不能同时较小，因为这两个互为逆，一个大另一个肯定小。（严格来说可以实现

，但显然这么做非常愚蠢）

Remark2：既然

需要和

互质，

可取的最小值为3，taking

is as secure as taking a larger value of

，

太小的人通常会采用

• 参见：

D. Boneh, R. Venkatesan, Breaking RSA may not be equivalent to factoring (extended abstract), in Advances in Cryptology—EUROCRYPT ’98, Espoo. Volume 1403 of Lecture Notes in Computer Science (Springer, Berlin, 1998), pp. 59–71

Remark3：Bob 的另一种选择是采用较小的

和较大的

，但这样可能导致安全漏洞。More precisely, if d is smaller than N1/4, then the theory of continued fractions allows Eve to break RSA.

• 参见：

J. Blo ̈mer, A. May, Low secret exponent RSA revisited, in Cryptography and Lattices, Providence, 2001. Volume 2146 of Lecture Notes in Computer Science (Springer, Berlin, 2001), pp. 4–19
D. Boneh, G. Durfee, Cryptanalysis of RSA with private key d less than

, in Advances in Cryptology—EUROCRYPT ’99, Prague. Volume 1592 of Lec- ture Notes in Computer Science (Springer, Berlin, 1999), pp. 1–11

D. Boneh, G. Durfee, Cryptanalysis of RSA with private key d less than

IEEE Trans. Inf. Theory 46(4), 1339–1349 (2000)

M. J. Wiener, Cryptanalysis of short RSA secret exponents. IEEE Trans. Inf. Theory 36(3), 553–558 (1990)

Remark4：从上一节的 Proposition2 看出，若 Eve 知道

的值，则他可以求解

(mod

) ，Bob 的公钥已经包括

，若 Eve 能得知

的值，则可轻松求出

，因为

。此外，若同时了解

的值还能分别求出

的值（利用韦达定理构造二次式）

Remark5：已知 “it is no easier for Eve to determine

than it is for her to factor

”。但这并不说明解密一定需要 factor

。真正重要的是解

(mod

) ，可能存在未知而有效的算法在不知道

的前提下求解。这种算法是否存在暂时未知，但有一个 suggestion that computing roots modulo

may be easier than factoring

• 参见：

D. Boneh, R. Venkatesan, Breaking RSA may not be equivalent to factoring (extended abstract), in Advances in Cryptology—EUROCRYPT ’98, Espoo. Volume 1403 of Lecture Notes in Computer Science (Springer, Berlin, 1998), pp. 59–71

注：上面所有 Remark 里面的参见仅是教材中参考文献的列举，笔者水平所限其实并没有读过

3.3 Implementation and Security Issues

中间人攻击 aka. MITM

前提：Eve 不仅是一个窃听者，同时对 Alice 和 Bob 的通信网络有完全控制权

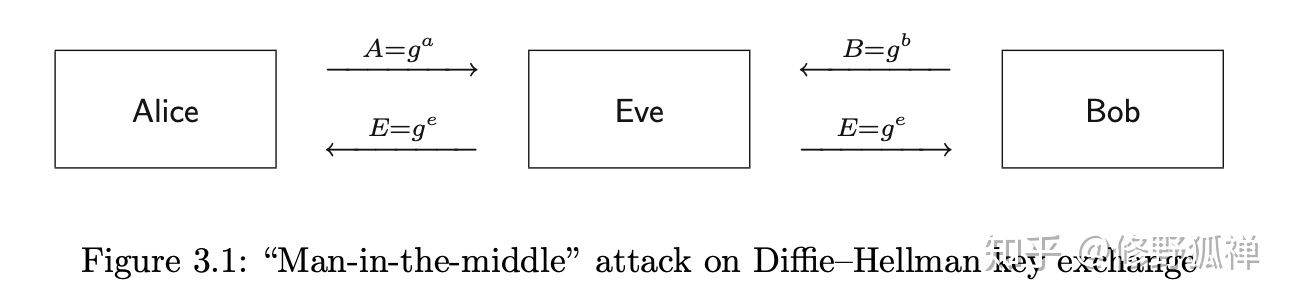
假设 Alice 和 Bob 利用 DH 交换后的

作为对称加密的密钥，则 Alice 用

加密原文

，Eve 拦截密文并用

解密，阅读后再用

重新加密发送给 Bob ，不知情的 Bob 用

解密，he is unaware that there is a breach in security

• 注意此攻击的隐秘性，在 MITM 中 Eve 无法解决 hard mathematical problems ，但却能够解密密文，而通信双方无法意识到这一点。

RSA

如果 Eve 能说服 Alice 用她的私钥解密随机的 RSA 信息，or Eve has access to an RSA oracle ，则：

1. 假设 Eve 已截获 Bob 的密文
   ，他可以选择随机数
   ，将信息
   (mod
   ) 发送给 Alice
2. Alice 解密
   并返回结果
   ，
   (mod
   )
3. 既然
   是 Eve 本人定的，他自然能读取原文

这个例子中值得注意的有：

• 加密系统中的困难数学问题被绕过，根本未发挥任何作用
• 既然 Eve 掩盖了 Bob 的原密文，Alice 也无法发现这次攻击

那么，没有这个 oracle 的情况下要怎么中间人攻击 RSA 密码系统呢 ？

答案是在双方公钥传输时发动

如果对于一个给定的 modulus

Alice 发布了两个 encryption exponent ，那这个加密加了和没加一样。

• 假设 Eve 截获两个密文
  (mod
  ) 和
  (mod
  )
• 则取一组
  满足方程
• 计算
  (mod
  )
• 如果
  ，那么原文就是裸奔的

推广：if several exponents

，can recover if

对于一个 modulus 只应该使用最多一个 encryption exponent

3.4 Primality Testing

更新中......