如何把密度函数化为标准正态二维分布_概率论复习(4): 正态分布
本节目录
- 正态分布和相关定义
- 一元正态分布的性质
- 多元正态分布的性质
正态分布和相关定义
首先是一个重要的积分, 即泊松积分, 它在求有关正态分布的一些量时往往有强大的作用.
引理4.1.1 设
注记 (1). 特别地, 令,
可得
![]()
(2). 该引理可以利用留数定理证明; 但也有相对初等的办法, 见课本pp132和pp252.
定义4.1.2 若随机变量
其中
注记 (1). 要验证的确是一个密度函数, 只需要应用引理4.1.1即可.
(2). 正态分布的分布函数![]()
不是一个初等函数.
(3). 习惯上将服从正态分布的随机变量称为 正态变量.
(4). 分布函数为单点分布 [1]可以看作退化的正态分布的
, 正态分布满足的性质退化分布也能算进来.
(5). 课本pp156-157说明了正态分布是如何导出的.
标准正态分布的密度函数一般记为
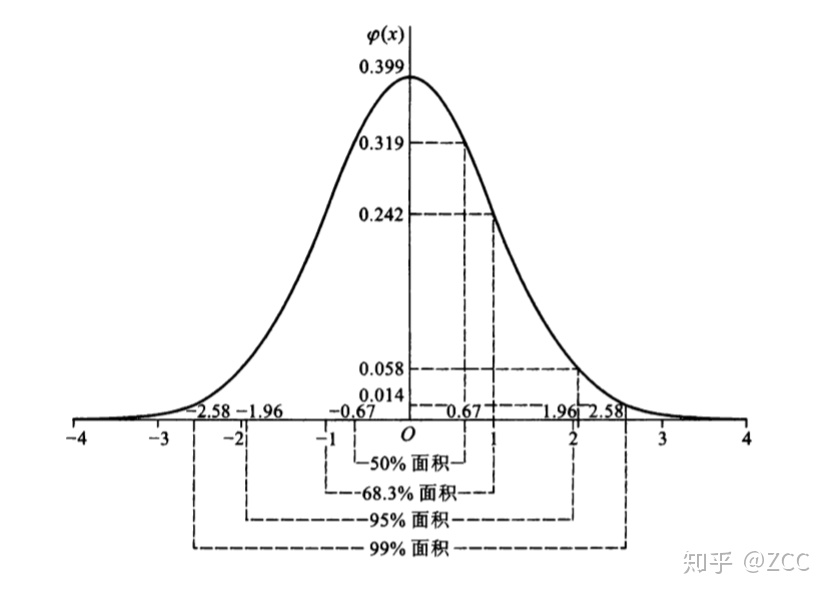
相应的分布函数一般记为
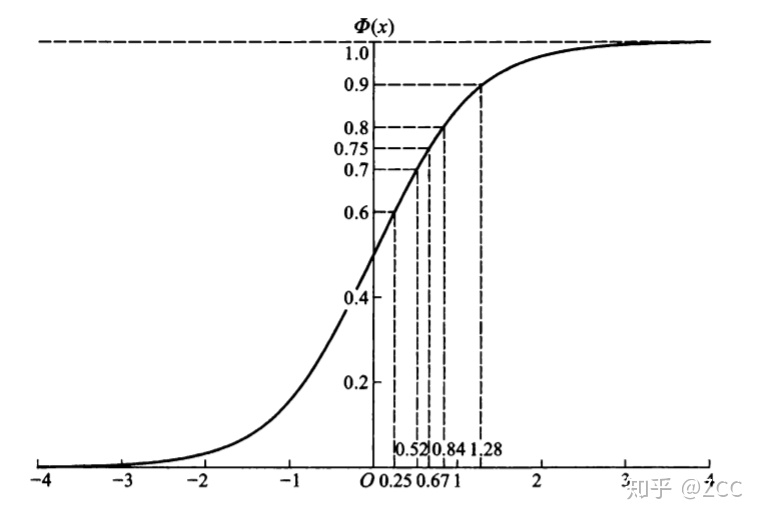
一元正态分布的性质
下设
定理4.2.1
证明 先考虑的情况.
利用柯西判别法能确定在
上绝对可积, 又
是一个奇函数, 因此
存在且等于
.
利用柯西判别法能确定在
上绝对可积, 因此二阶原点矩
存在, 且易得
![]()
利用分部积分和引理4.1.1即可得, 从而
.
利用公式![]()
和![]()
即可得在一般情况有
,
注记 在求连续型随机变量的矩时务必先验证相应函数是绝对可积的. 课本是直接按一般情况求的期望和方差, 这里利用期望和方差的性质能略微减少计算的难度..
定理4.2.2
证明 先考虑标准化了的, 这时
![]()
利用可知
![]()
利用引理4.1.1知上式等于.
而由于是(关于
)的奇函数, 因此易得
![]()
(注意, 上面的几个广义积分我们都略去了验证绝对可积这一步骤)
因此.
利用即得要证等式.
对于某种分布(例如正态分布), 如果一对相互独立的随机变量
定理4.2.3 正态分布具有再生性. 事实上, 若
只需看和
的乘积即可.
多元正态分布的性质
我们先来看二维正态分布.
定义4.3.1 若随机向量
则称
注记 (1).有典型分解
![]()
可以注意到等号右边, 前一部分是的密度函数, 后一部分是
的密度函数. 对称地可以把相应参数进行对换.
(2). 利用典型分解可以说明![]()
即二元正态分布的边际分布也是正态分布.
定理4.3.2 在定义4.3.1的叙述中,
证明和
的协方差为
![]()
作变量代换![]()
则上述重积分化为![]()
上面被积分的函数可以表达为形如的形式, 这时可以求得
, 因此相关系数为
注记 求二元正态分布相关的量一定要熟悉一些变量代换..
注意到
因此可知
推论4.3.3 对于服从二元正态分布的随机向量
课本上pp212的 [例9] 作为反例是值得注意的, 囿于篇幅不再赘述.
现在我们来定义一般的多元正态分布.
定义4.3.4 考虑两个列向量
这里矩阵的上标中
可以验证(课本pp261)![]()
若存在某一
定理4.3.5
定理4.3.6
注记 在上式中如果把放宽半正定的条件, 则可以拓宽定义4.3.4中正态分布的范围. 当
时,
可以看作称为一个
维子空间上的概率分布, 这类分布称为退化正态分布.
推论4.3.7 考虑
这里
推论4.3.8
定理4.3.9(线性变换不变性) 设
条件分布的内容从略, 见课本pp269-271.
正态分布相当典型, 题目也相当多. 如果有不足之处欢迎指出. 下一节我们整理其他典型分布, 除了熟悉的二项分布、泊松分布、超几何分布, 我们还要整理
参考
- ^也叫退化分布, 即随机变量取值只有某个常数c的分布.
- ^标准化的概念是上一节引入的, 但注意我们这时还没有说明正态分布的两个参数μ和σ是期望和方差. 不过通过这一线性变换能将一般正态分布化为标准正态分布是容易验证的.
