西瓜书研读——第四章 决策树:ID3、C4.2、CSRT算法
西瓜书研读系列:
西瓜书研读——第三章 线性模型:一元线性回归
西瓜书研读——第三章 线性模型:多元线性回归
西瓜书研读——第三章 线性模型:线性几率回归(逻辑回归)
西瓜书研读——第三章 线性模型: 线性判别分析 LDA
- 主要教材为西瓜书,结合南瓜书,统计学习方法,B站视频整理~
- 人群定位:学过高数会求偏导、线代会矩阵运算、概率论知道啥是概率
- 原理讲解,公式推导,课后习题,实践代码应有尽有,欢迎订阅
文章目录
- 4 决策树
- 4.1 基本概念与构造流程
- 4.2 划分选择
- 4.2.1 信息增益 ( ID3算法)
- 4.2.2 增益率 (C4.5算法)
- 4.2.3 基尼指数( CART算法)
4 决策树
决策树(Decision Tree)是一种非参数的有监督学习方法,它能够从一系列有特征和标签的数据中总结出决策规则,并用树状图的结构来呈现这些规则,以解决分类和回归问题,决策树算法的本质是一种图结构。
决策树算法容易理解,适用各种数据,在解决各种问题时都有良好表现,尤其是以树模型为核心的各种集成算法,在各个行业和领域都有广泛的应用。
4.1 基本概念与构造流程
以西瓜数据集为例,决策树是如何生成的?
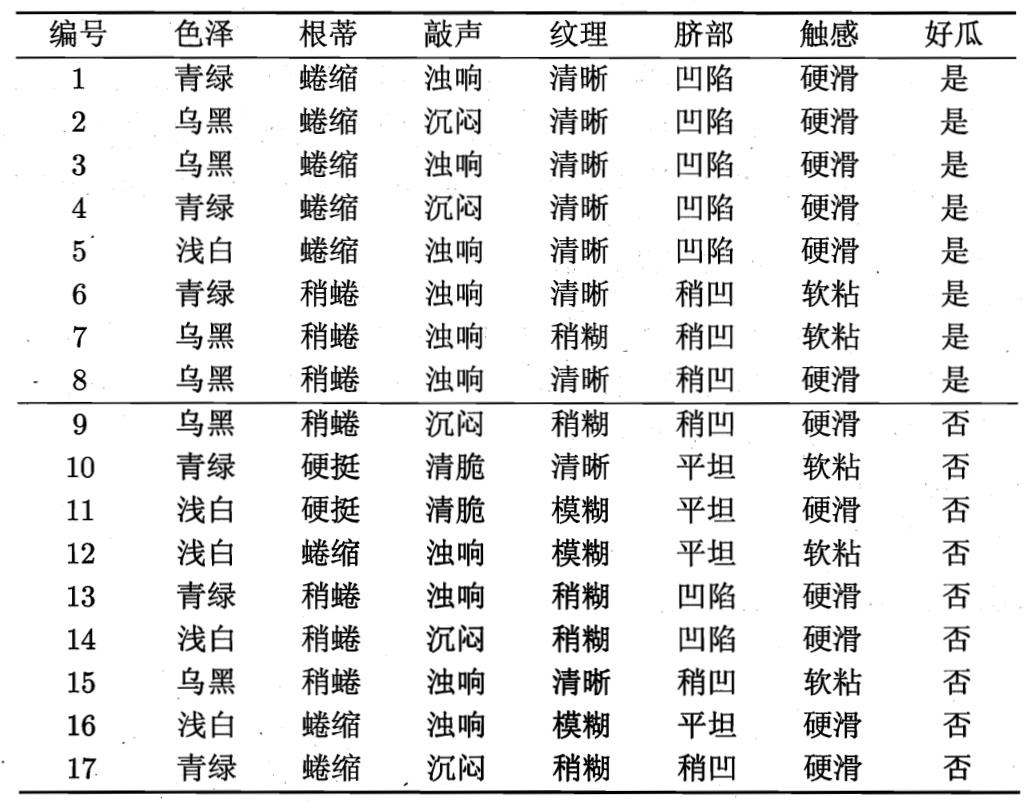
在上图的决策树中,决策过程的每一次判定都是对某一属性的“测试”,决策最终结论则对应最终的判定结果。一般一棵决策树包含:一个根节点、若干个内部节点和若干个叶子节点,易知:
- 非叶节点:表示一个特征属性测试。
- 分支:代表这个特征属性在某个值域上的输出。
- 叶子节点:存放一个类别。
每个结点包含的样本集合根据属性测试的结果被划分到子结点中,而根结点包含了样本全集。
从根结点到每个叶结点的路径对应了一个判定测试序列
构造流程

决策树的生成是一个递归过程
三种会导致递归返回的情形
- 当前结点包含的样本全属于同一类别,无需划分
- 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分
- 把当前结点标记为叶结点,并将其类别设定为该结点所含样本最多的类别
- 利用当前结点的后验分布
- 当前结点包含的样本集合为空,不能划分
- 把当前结点标记为叶结点,但将其类别设定为父结点所含样本做多的类别
- 把父结点的样本分布作为当前结点的先验分布
决策树各类算法的核心就就在于:如何解决“从A中选择最优划分属性”?
4.2 划分选择
核心问题:如何解决“从A中选择最优划分属性”?
划分目的:决策树分支结点所包含的样本尽可能属于同一类别,即结点的“纯度”(purity)越来越高
点击查看信息论补充知识

信息熵(information entropy)
在决策树种,信息熵通常是用来度量样本集合纯度最常用的一种指标,信息量越大 信息熵越大,不确定性越大。
Ent
(
D
)
=
−
∑
k
=
1
∣
Y
∣
p
k
log
2
p
k
\operatorname{Ent}(D)=-\sum_{k=1}^{|\mathcal{Y}|}p_k\log_{2}{p_k}
Ent(D)=−k=1∑∣Y∣pklog2pk
条件熵:表示的是在已知一个随机变量的条件下,另一个随机变量的不确定性。
具体地,假设有随机变量
X
X
X和
Y
Y
Y,且它们服从以下联合概率分布
P
(
X
=
x
i
,
Y
=
y
j
)
=
p
i
j
i
=
1
,
2
,
.
.
.
.
,
n
;
j
=
1
,
2
,
.
.
.
,
m
P(X = x_{i},Y = y_{j}) = p_{ij}\quad i = 1,2,....,n;j = 1,2,...,m
P(X=xi,Y=yj)=piji=1,2,....,n;j=1,2,...,m
那么在已知
X
X
X的条件下,随机变量
Y
Y
Y的条件熵为
H
(
Y
∣
X
)
=
∑
x
p
(
x
)
H
(
Y
∣
X
=
x
)
H(Y|X)=\sum_{x}p(x)H(Y|X=x)
H(Y∣X)=x∑p(x)H(Y∣X=x)
Ent ( Y ∣ X ) = ∑ i = 1 n p i Ent ( Y ∣ X = x i ) \operatorname{Ent}(Y|X) = \sum_{i=1}^np_i \operatorname{Ent}(Y|X = x_i) Ent(Y∣X)=i=1∑npiEnt(Y∣X=xi)
其中,$ p_i = P(X = x_i) ,i =1,2,…,n$。
在信息论中信息增益也称为互信息
互信息:信息熵和条件熵的差,它表示的是已知一个随机变量的信息后使得另一个随机变量的不确定性减少的程度。
具体地,假设有随机变量
X
X
X和
Y
Y
Y,那么在已知
X
X
X的信息后,
Y
Y
Y的不确定性减少的程度为
I
(
Y
;
X
)
=
Ent
(
Y
)
−
Ent
(
Y
∣
X
)
\operatorname{I}(Y;X) = \operatorname{Ent}(Y) - \operatorname{Ent}(Y|X)
I(Y;X)=Ent(Y)−Ent(Y∣X)
此即为互信息的数学定义。
证明 0 ≤ Ent ( D ) ≤ log 2 ∣ Y ∣ 0\leq\operatorname{Ent}(D)\leq\log_{2}|\mathcal{Y}| 0≤Ent(D)≤log2∣Y∣:
已知集合
D
D
D的信息熵的定义为
Ent
(
D
)
=
−
∑
k
=
1
∣
Y
∣
p
k
log
2
p
k
\operatorname{Ent}(D)=-\sum_{k=1}^{|\mathcal{Y}|} p_{k} \log _{2} p_{k}
Ent(D)=−k=1∑∣Y∣pklog2pk
其中,
∣
Y
∣
|\mathcal{Y}|
∣Y∣表示样本类别总数,
p
k
p_k
pk表示第
k
k
k类样本所占的比例,且
0
≤
p
k
≤
1
,
∑
k
=
1
n
p
k
=
1
0 \leq p_k \leq 1,\sum_{k=1}^{n}p_k=1
0≤pk≤1,∑k=1npk=1。若令
∣
Y
∣
=
n
,
p
k
=
x
k
|\mathcal{Y}|=n,p_k=x_k
∣Y∣=n,pk=xk,那么信息熵
Ent
(
D
)
\operatorname{Ent}(D)
Ent(D)就可以看作一个
n
n
n元实值函数,也即
Ent
(
D
)
=
f
(
x
1
,
.
.
.
,
x
n
)
=
−
∑
k
=
1
n
x
k
log
2
x
k
\operatorname{Ent}(D)=f(x_1,...,x_n)=-\sum_{k=1}^{n} x_{k} \log _{2} x_{k}
Ent(D)=f(x1,...,xn)=−k=1∑nxklog2xk
其中,
0
≤
x
k
≤
1
,
∑
k
=
1
n
x
k
=
1
0 \leq x_k \leq 1,\sum_{k=1}^{n}x_k=1
0≤xk≤1,∑k=1nxk=1,下面考虑求该多元函数的最值。首先我们先来求最大值,如果不考虑约束
0
≤
x
k
≤
1
0 \leq x_k \leq 1
0≤xk≤1,仅考虑
∑
k
=
1
n
x
k
=
1
\sum_{k=1}^{n}x_k=1
∑k=1nxk=1的话,对
f
(
x
1
,
.
.
.
,
x
n
)
f(x_1,...,x_n)
f(x1,...,xn)求最大值等价于如下最小化问题
min
∑
k
=
1
n
x
k
log
2
x
k
s.t.
∑
k
=
1
n
x
k
=
1
\begin{array}{ll}{ \operatorname{min}} & {\sum\limits_{k=1}^{n} x_{k} \log _{2} x_{k} } \\ {\text { s.t. }} & {\sum\limits_{k=1}^{n}x_k=1} \end{array}
min s.t. k=1∑nxklog2xkk=1∑nxk=1
显然,在
0
≤
x
k
≤
1
0 \leq x_k \leq 1
0≤xk≤1时,此问题为凸优化问题,而对于凸优化问题来说,能令其拉格朗日函数的一阶偏导数等于0的点即为最优解。根据拉格朗日乘子法可知,该优化问题的拉格朗日函数为
L
(
x
1
,
.
.
.
,
x
n
,
λ
)
=
∑
k
=
1
n
x
k
log
2
x
k
+
λ
(
∑
k
=
1
n
x
k
−
1
)
L(x_1,...,x_n,\lambda)=\sum_{k=1}^{n} x_{k} \log _{2} x_{k}+\lambda(\sum_{k=1}^{n}x_k-1)
L(x1,...,xn,λ)=k=1∑nxklog2xk+λ(k=1∑nxk−1)
其中,
λ
\lambda
λ为拉格朗日乘子。对
L
(
x
1
,
.
.
.
,
x
n
,
λ
)
L(x_1,...,x_n,\lambda)
L(x1,...,xn,λ)分别关于
x
1
,
.
.
.
,
x
n
,
λ
x_1,...,x_n,\lambda
x1,...,xn,λ求一阶偏导数,并令偏导数等于0可得
∂
L
(
x
1
,
.
.
.
,
x
n
,
λ
)
∂
x
1
=
∂
∂
x
1
[
∑
k
=
1
n
x
k
log
2
x
k
+
λ
(
∑
k
=
1
n
x
k
−
1
)
]
=
0
=
log
2
x
1
+
x
1
⋅
1
x
1
ln
2
+
λ
=
0
=
log
2
x
1
+
1
ln
2
+
λ
=
0
⇒
λ
=
−
log
2
x
1
−
1
ln
2
∂
L
(
x
1
,
.
.
.
,
x
n
,
λ
)
∂
x
2
=
∂
∂
x
2
[
∑
k
=
1
n
x
k
log
2
x
k
+
λ
(
∑
k
=
1
n
x
k
−
1
)
]
=
0
⇒
λ
=
−
log
2
x
2
−
1
ln
2
⋮
∂
L
(
x
1
,
.
.
.
,
x
n
,
λ
)
∂
x
n
=
∂
∂
x
n
[
∑
k
=
1
n
x
k
log
2
x
k
+
λ
(
∑
k
=
1
n
x
k
−
1
)
]
=
0
⇒
λ
=
−
log
2
x
n
−
1
ln
2
∂
L
(
x
1
,
.
.
.
,
x
n
,
λ
)
∂
λ
=
∂
∂
λ
[
∑
k
=
1
n
x
k
log
2
x
k
+
λ
(
∑
k
=
1
n
x
k
−
1
)
]
=
0
⇒
∑
k
=
1
n
x
k
=
1
\begin{aligned} \cfrac{\partial L(x_1,...,x_n,\lambda)}{\partial x_1}&=\cfrac{\partial }{\partial x_1}\left[\sum_{k=1}^{n} x_{k} \log _{2} x_{k}+\lambda(\sum_{k=1}^{n}x_k-1)\right]=0\\ &=\log _{2} x_{1}+x_1\cdot \cfrac{1}{x_1\ln2}+\lambda=0 \\ &=\log _{2} x_{1}+\cfrac{1}{\ln2}+\lambda=0 \\ &\Rightarrow \lambda=-\log _{2} x_{1}-\cfrac{1}{\ln2}\\ \cfrac{\partial L(x_1,...,x_n,\lambda)}{\partial x_2}&=\cfrac{\partial }{\partial x_2}\left[\sum_{k=1}^{n} x_{k} \log _{2} x_{k}+\lambda(\sum_{k=1}^{n}x_k-1)\right]=0\\ &\Rightarrow \lambda=-\log _{2} x_{2}-\cfrac{1}{\ln2}\\ \vdots\\ \cfrac{\partial L(x_1,...,x_n,\lambda)}{\partial x_n}&=\cfrac{\partial }{\partial x_n}\left[\sum_{k=1}^{n} x_{k} \log _{2} x_{k}+\lambda(\sum_{k=1}^{n}x_k-1)\right]=0\\ &\Rightarrow \lambda=-\log _{2} x_{n}-\cfrac{1}{\ln2}\\ \cfrac{\partial L(x_1,...,x_n,\lambda)}{\partial \lambda}&=\cfrac{\partial }{\partial \lambda}\left[\sum_{k=1}^{n} x_{k} \log _{2} x_{k}+\lambda(\sum_{k=1}^{n}x_k-1)\right]=0\\ &\Rightarrow \sum_{k=1}^{n}x_k=1\\ \end{aligned}
∂x1∂L(x1,...,xn,λ)∂x2∂L(x1,...,xn,λ)⋮∂xn∂L(x1,...,xn,λ)∂λ∂L(x1,...,xn,λ)=∂x1∂[k=1∑nxklog2xk+λ(k=1∑nxk−1)]=0=log2x1+x1⋅x1ln21+λ=0=log2x1+ln21+λ=0⇒λ=−log2x1−ln21=∂x2∂[k=1∑nxklog2xk+λ(k=1∑nxk−1)]=0⇒λ=−log2x2−ln21=∂xn∂[k=1∑nxklog2xk+λ(k=1∑nxk−1)]=0⇒λ=−log2xn−ln21=∂λ∂[k=1∑nxklog2xk+λ(k=1∑nxk−1)]=0⇒k=1∑nxk=1
整理一下可得
{
λ
=
−
log
2
x
1
−
1
ln
2
=
−
log
2
x
2
−
1
ln
2
=
.
.
.
=
−
log
2
x
n
−
1
ln
2
∑
k
=
1
n
x
k
=
1
\left\{ \begin{array}{lr} \lambda=-\log _{2} x_{1}-\cfrac{1}{\ln2}=-\log _{2} x_{2}-\cfrac{1}{\ln2}=...=-\log _{2} x_{n}-\cfrac{1}{\ln2} \\ \sum\limits_{k=1}^{n}x_k=1 \end{array}\right.
⎩
⎨
⎧λ=−log2x1−ln21=−log2x2−ln21=...=−log2xn−ln21k=1∑nxk=1
由以上两个方程可以解得
x
1
=
x
2
=
.
.
.
=
x
n
=
1
n
x_1=x_2=...=x_n=\cfrac{1}{n}
x1=x2=...=xn=n1
又因为
x
k
x_k
xk还需满足约束
0
≤
x
k
≤
1
0 \leq x_k \leq 1
0≤xk≤1,显然
0
≤
1
n
≤
1
0 \leq\cfrac{1}{n}\leq 1
0≤n1≤1,所以
x
1
=
x
2
=
.
.
.
=
x
n
=
1
n
x_1=x_2=...=x_n=\cfrac{1}{n}
x1=x2=...=xn=n1是满足所有约束的最优解,也即为当前最小化问题的最小值点,同时也是
f
(
x
1
,
.
.
.
,
x
n
)
f(x_1,...,x_n)
f(x1,...,xn)的最大值点。将
x
1
=
x
2
=
.
.
.
=
x
n
=
1
n
x_1=x_2=...=x_n=\cfrac{1}{n}
x1=x2=...=xn=n1代入
f
(
x
1
,
.
.
.
,
x
n
)
f(x_1,...,x_n)
f(x1,...,xn)中可得
f
(
1
n
,
.
.
.
,
1
n
)
=
−
∑
k
=
1
n
1
n
log
2
1
n
=
−
n
⋅
1
n
log
2
1
n
=
log
2
n
f(\cfrac{1}{n},...,\cfrac{1}{n})=-\sum_{k=1}^{n} \cfrac{1}{n} \log _{2} \cfrac{1}{n}=-n\cdot\cfrac{1}{n} \log _{2} \cfrac{1}{n}=\log _{2} n
f(n1,...,n1)=−k=1∑nn1log2n1=−n⋅n1log2n1=log2n
所以显然
f
(
x
1
,
.
.
.
,
x
n
)
f(x_1,...,x_n)
f(x1,...,xn)在满足约束
0
≤
x
k
≤
1
,
∑
k
=
1
n
x
k
=
1
0 \leq x_k \leq 1,\sum_{k=1}^{n}x_k=1
0≤xk≤1,∑k=1nxk=1时的最大值为
log
2
n
\log _{2} n
log2n。
求完最大值后下面我们再来求最小值,如果不考虑约束
∑
k
=
1
n
x
k
=
1
\sum_{k=1}^{n}x_k=1
∑k=1nxk=1,仅考虑
0
≤
x
k
≤
1
0 \leq x_k \leq 1
0≤xk≤1的话,
f
(
x
1
,
.
.
.
,
x
n
)
f(x_1,...,x_n)
f(x1,...,xn)可以看做是
n
n
n个互不相关的一元函数的加和,也即
f
(
x
1
,
.
.
.
,
x
n
)
=
∑
k
=
1
n
g
(
x
k
)
f(x_1,...,x_n)=\sum_{k=1}^{n} g(x_k)
f(x1,...,xn)=k=1∑ng(xk)
其中,
g
(
x
k
)
=
−
x
k
log
2
x
k
,
0
≤
x
k
≤
1
g(x_k)=-x_{k} \log _{2} x_{k},0 \leq x_k \leq 1
g(xk)=−xklog2xk,0≤xk≤1。那么当
g
(
x
1
)
,
g
(
x
2
)
,
.
.
.
,
g
(
x
n
)
g(x_1),g(x_2),...,g(x_n)
g(x1),g(x2),...,g(xn)分别取到其最小值时,
f
(
x
1
,
.
.
.
,
x
n
)
f(x_1,...,x_n)
f(x1,...,xn)也就取到了最小值。所以接下来考虑分别求
g
(
x
1
)
,
g
(
x
2
)
,
.
.
.
,
g
(
x
n
)
g(x_1),g(x_2),...,g(x_n)
g(x1),g(x2),...,g(xn)
各自的最小值,由于 g ( x 1 ) , g ( x 2 ) , . . . , g ( x n ) g(x_1),g(x_2),...,g(x_n) g(x1),g(x2),...,g(xn)的定义域和函数表达式均相同,所以只需求出 g ( x 1 ) g(x_1) g(x1)的最小值也就求出了 g ( x 2 ) , . . . , g ( x n ) g(x_2),...,g(x_n) g(x2),...,g(xn)的最小值。下面考虑求 g ( x 1 ) g(x_1) g(x1)的最小值,首先对 g ( x 1 ) g(x_1) g(x1)关于 x 1 x_1 x1求一阶和二阶导数
g ′ ( x 1 ) = d ( − x 1 log 2 x 1 ) d x 1 = − log 2 x 1 − x 1 ⋅ 1 x 1 ln 2 = − log 2 x 1 − 1 ln 2 g^{\prime}(x_1)=\cfrac{d(-x_{1} \log _{2} x_{1})}{d x_1}=-\log _{2} x_{1}-x_1\cdot \cfrac{1}{x_1\ln2}=-\log _{2} x_{1}-\cfrac{1}{\ln2} g′(x1)=dx1d(−x1log2x1)=−log2x1−x1⋅x1ln21=−log2x1−ln21
g
′
′
(
x
1
)
=
d
(
g
′
(
x
1
)
)
d
x
1
=
d
(
−
log
2
x
1
−
1
ln
2
)
d
x
1
=
−
1
x
1
ln
2
g^{\prime\prime}(x_1)=\cfrac{d\left(g^{\prime}(x_1)\right)}{d x_1}=\cfrac{d\left(-\log _{2} x_{1}-\cfrac{1}{\ln2}\right)}{d x_1}=-\cfrac{1}{x_{1}\ln2}
g′′(x1)=dx1d(g′(x1))=dx1d(−log2x1−ln21)=−x1ln21
显然,当
0
≤
x
k
≤
1
0 \leq x_k \leq 1
0≤xk≤1时
g
′
′
(
x
1
)
=
−
1
x
1
ln
2
g^{\prime\prime}(x_1)=-\cfrac{1}{x_{1}\ln2}
g′′(x1)=−x1ln21恒小于0,所以
g
(
x
1
)
g(x_1)
g(x1)是一个在其定义域范围内开口向下的凹函数,那么其最小值必然在边界取,于是分别取
x
1
=
0
x_1=0
x1=0和
x
1
=
1
x_1=1
x1=1,代入
g
(
x
1
)
g(x_1)
g(x1)可得
g
(
0
)
=
−
0
log
2
0
=
0
g
(
1
)
=
−
1
log
2
1
=
0
g(0)=-0\log _{2} 0=0 \\ g(1)=-1\log _{2} 1=0
g(0)=−0log20=0g(1)=−1log21=0
所以,
g
(
x
1
)
g(x_1)
g(x1)的最小值为0,同理可得
g
(
x
2
)
,
.
.
.
,
g
(
x
n
)
g(x_2),...,g(x_n)
g(x2),...,g(xn)的最小值也为0,那么
f
(
x
1
,
.
.
.
,
x
n
)
f(x_1,...,x_n)
f(x1,...,xn)的最小值此时也为0。
综上可知,当 f ( x 1 , . . . , x n ) f(x_1,...,x_n) f(x1,...,xn)取到最大值时: x 1 = x 2 = . . . = x n = 1 n x_1=x_2=...=x_n=\cfrac{1}{n} x1=x2=...=xn=n1,此时样本集合纯度最低;当 f ( x 1 , . . . , x n ) f(x_1,...,x_n) f(x1,...,xn)取到最小值时: x k = 1 , x 1 = x 2 = . . . = x k − 1 = x k + 1 = . . . = x n = 0 x_k=1,x_1=x_2=...=x_{k-1}=x_{k+1}=...=x_n=0 xk=1,x1=x2=...=xk−1=xk+1=...=xn=0,此时样本集合纯度最高。
- Ent ( D ) \text{Ent}(D) Ent(D) 的值越小,则 D D D 的纯度越高
- Ent ( D ) \text{Ent}(D) Ent(D) 的最小值为0,最大值为 log 2 ∣ Y ∣ \log_2|\mathcal{Y}| log2∣Y∣
4.2.1 信息增益 ( ID3算法)
一般而言,信息增益越大,即取值后样本集的不确定性减小的程度越大,则意味着使用属性𝒂进行划分所获得的“纯度提升”越大。
ID3算法使用信息增益为准则来选择划分属性。
假定离散属性a(比如西瓜色泽)有V个可能的取值
{
a
1
,
a
2
,
…
,
a
V
}
\{a^1,a^2,\dots,a^V\}
{a1,a2,…,aV}(给色泽打分,分别是1 2 3…V),
D
k
D^k
Dk表示属性
a
a
a取值为
a
k
∈
{
a
1
,
a
2
,
…
,
a
V
}
a^k \in \{a^1,a^2,\dots,a^V\}
ak∈{a1,a2,…,aV}的样本集合(即色泽打分为
a
k
a^k
ak的所有瓜),
∣
D
k
∣
∣
D
∣
\frac{|D^k|}{|D|}
∣D∣∣Dk∣表示占比(色泽为
a
k
a^k
ak的瓜在所有瓜中的占比),那么在已知属性a的取值后,样本集合D的条件熵为:
∑
k
=
1
V
∣
D
k
∣
∣
D
∣
Ent
(
D
k
)
\sum_{k=1}^{V}\frac{|D^k|}{|D|}\operatorname{Ent}({D^k})
k=1∑V∣D∣∣Dk∣Ent(Dk)
分支节点包含的样本数越多,表示该分支节点的影响力越大。故可以计算出划分后相比原始数据集D获得的“信息增益”(information gain)。
Gain
(
D
,
a
)
=
Ent
(
D
)
−
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
Ent
(
D
v
)
(4.2)
\operatorname{Gain}(D,a) = \operatorname{Ent}(D) - \sum_{v=1}^{V}\frac{|D^v|}{|D|}\operatorname{Ent}({D^v}) \tag{4.2}
Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)(4.2)
这个是信息增益的定义公式,在信息论中信息增益也称为互信息,其表示已知一个随机变量的信息后使得另一个随机变量的不确定性减少的程度。
所以在这里,这个公式可以理解为在属性 a a a的取值已知后,样本类别这个随机变量的不确定性减小的程度。
信息增益越大,说明在知道其取值后样本集的不确定性减小的程度越大,也即为书上所说的“纯度提升”越大,表示使用该属性划分样本集D的效果越好,因此ID3算法在递归过程中,每次选择最大信息增益的属性作为当前的划分属性。
西瓜例子:
计算过程:
西瓜数据集共17个训练样本,类别 𝒚 = 𝟐;其中正例占𝒑𝟏 = 𝟖/𝟏𝟕,反例占𝒑𝟐 = 𝟗/𝟏𝟕。
根结点信息熵为:
Ent
(
D
)
=
−
∑
k
=
1
2
p
k
log
2
p
k
=
−
(
8
17
log
2
8
17
+
9
17
log
2
9
17
)
=
0.998
\text{Ent}(D)=-\sum_{k=1}^2p_k\log_2p_k=-(\frac{8}{17}\log_2\frac{8}{17}+\frac{9}{17}\log_2\frac{9}{17})=0.998
Ent(D)=−k=1∑2pklog2pk=−(178log2178+179log2179)=0.998
然后计算当前属性集合{色泽,根蒂,敲声,纹理,脐部,触感}中每个属性的信息增益。
例如以“色泽”作为划分依据,取值{青绿,乌黑,浅白},若使用该属性对𝑫进行划分,则可得3个子集,分别标记为:𝑫𝟏(色泽=青绿)、𝑫𝟐(色泽=乌黑)、 𝑫𝟑(色泽=浅白)则可以建立三个分支其对应的信息熵。
子集𝑫𝟏中共6个样本,正例占𝒑𝟏 = 𝟑/𝟔,反例占𝒑𝟐 = 𝟑/𝟔,其他两个子集类似计算占比,则“色泽”划分之后所获得的3个分支结点的信息熵为
Ent ( D 1 ) = − ( 3 6 log 2 3 6 + 3 6 log 2 3 6 ) = 1.000 \text{Ent}(D^1)=-(\frac{3}{6}\log_2\frac{3}{6}+\frac{3}{6}\log_2\frac{3}{6})=1.000 Ent(D1)=−(63log263+63log263)=1.000
Ent ( D 2 ) = − ( 4 6 log 2 4 6 + 2 6 log 2 2 6 ) = 0.918 \text{Ent}(D^2)=-(\frac{4}{6}\log_2\frac{4}{6}+\frac{2}{6}\log_2\frac{2}{6})=0.918 Ent(D2)=−(64log264+62log262)=0.918
Ent ( D 3 ) = − ( 1 5 log 2 1 5 + 4 5 log 2 4 5 ) = 0.722 \text{Ent}(D^3)=-(\frac{1}{5}\log_2\frac{1}{5}+\frac{4}{5}\log_2\frac{4}{5})=0.722 Ent(D3)=−(51log251+54log254)=0.722
则“色泽”对应的信息增益为
Gain ( D , 色泽 ) = Ent ( D ) − ∑ v = 1 3 ∣ D v ∣ ∣ D ∣ Ent ( D v ) = 0.998 − ( 6 17 × 1.000 + 6 17 × 0.918 + 5 17 × 0.722 ) = 0.109 \begin{align} \text{Gain}(D,色泽) &= \text{Ent}(D) - \sum_{v=1}^3\frac{|D^v|}{|D|}\text{Ent}(D^v) \\\\ &= 0.998 - (\frac{6}{17} \times {1.000} + \frac{6}{17} \times {0.918} + \frac{5}{17} \times {0.722}) \\\\ &= 0.109 \end{align} Gain(D,色泽)=Ent(D)−v=1∑3∣D∣∣Dv∣Ent(Dv)=0.998−(176×1.000+176×0.918+175×0.722)=0.109
类似的,其他属性对应的信息增益
Gain ( D , 根蒂 ) = 0.143 \text{Gain}(D,根蒂) = 0.143 Gain(D,根蒂)=0.143
Gain ( D , 敲声 ) = 0.141 \text{Gain}(D,敲声) = 0.141 Gain(D,敲声)=0.141
Gain ( D , 纹理 ) = 0.381 \text{Gain}(D,纹理) = 0.381 Gain(D,纹理)=0.381
Gain ( D , 脐部 ) = 0.289 \text{Gain}(D,脐部) = 0.289 Gain(D,脐部)=0.289
Gain ( D , 触感 ) = 0.006 \text{Gain}(D,触感) = 0.006 Gain(D,触感)=0.006
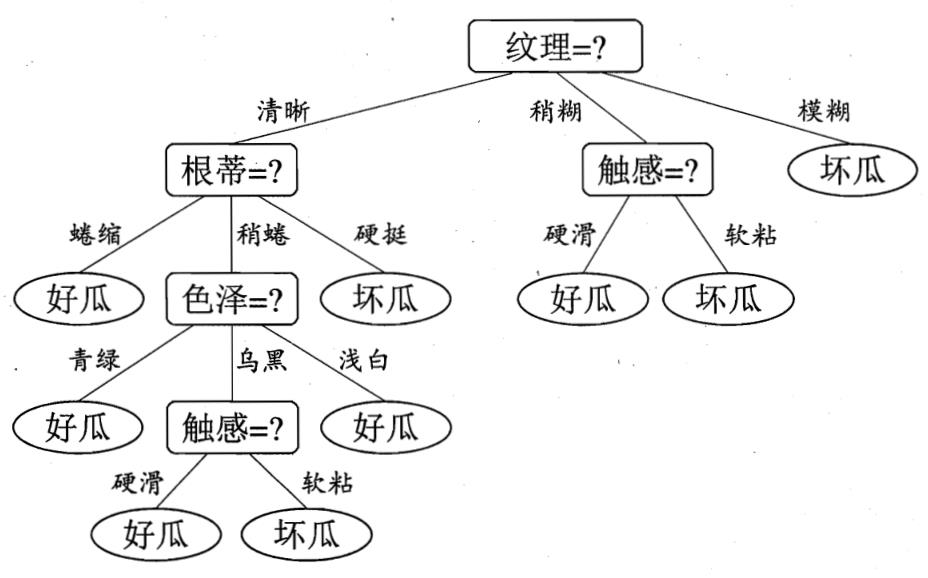
显然,属性“纹理”的信息增益最大,于是它被选为划分属性
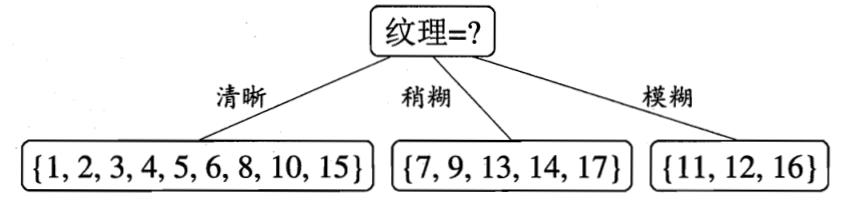
决策树学习算法将对每个分支结点进一步划分。以第一个分支结点(纹理=清晰)为例,该结点包含的样本集合𝑫𝟏有编号为{1, 2, 3, 4, 5, 6, 8, 10, 15}的9个样本,可用属性集合为{色泽,根蒂,敲声,脐部,触感}。基于𝑫𝟏计算各属性的信息增益
Gain
(
D
1
,
色泽
)
=
0.043
Gain
(
D
1
,
根蒂
)
=
0.458
Gain
(
D
1
,
敲声
)
=
0.331
Gain
(
D
1
,
脐部
)
=
0.458
Gain
(
D
1
,
触感
)
=
0.458
\operatorname{Gain}\left(D^{1}\right. , 色泽 )=0.043 \\ \operatorname{Gain}\left(D^{1}\right. , 根蒂 )=0.458 \\\operatorname{Gain}\left(D^{1}\right. , 敲声 )=0.331 \\ \operatorname{Gain}\left(D^{1}\right. , 脐部 )=0.458 \\\operatorname{Gain}\left(D^{1}\right. , 触感 )=0.458
Gain(D1,色泽)=0.043Gain(D1,根蒂)=0.458Gain(D1,敲声)=0.331Gain(D1,脐部)=0.458Gain(D1,触感)=0.458
“根蒂”、“脐部”和“触感”3个属性均取得最大的信息增益,可认选其中之一作为划分
属性。类似,对每个分支结点进行上述操作,最终得到决策树
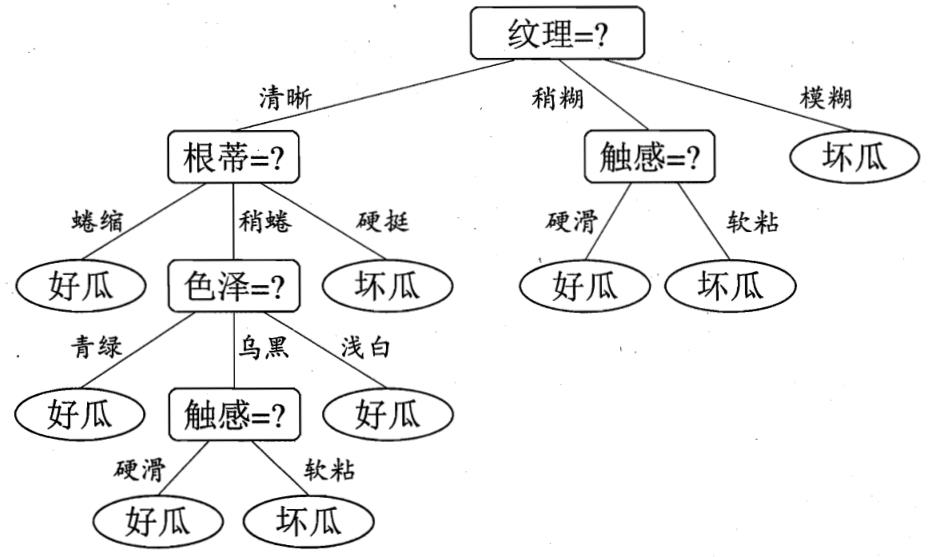
算法特点:
信息增益准则对可取值数目较多的属性有所偏好,因此其在选择分类属性的时候倾向混乱程度更大的属性
4.2.2 增益率 (C4.5算法)
ID3算法存在一个问题,就是偏向于取值数目较多的属性,例如:如果存在一个唯一标识,这样样本集D将会被划分为 ∣ D ∣ |D| ∣D∣个分支,每个分支只有一个样本,这样划分后的信息熵为零,十分纯净,但是对分类毫无用处。
C4.5算法使用了“增益率”(gain ratio)来选择划分属性。
增益率定义为:
Gain_ratio
(
D
,
a
)
=
Gain
(
D
,
a
)
IV
(
a
)
IV
(
a
)
=
−
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
log
2
∣
D
v
∣
∣
D
∣
\begin{align} & \text{Gain\_ratio}(D,a)=\frac{\text{Gain}(D,a)}{\text{IV}(a)} \\\\ & \text{IV}(a)=-\sum_{v=1}^V\frac{|D^v|}{|D|}\log_2\frac{|D^v|}{|D|} \end{align}
Gain_ratio(D,a)=IV(a)Gain(D,a)IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣
其中 IV ( a ) \text{IV}(a) IV(a) 称为属性 a a a 的固有值
属性a的可能取值数目越多(即V越大),则 I V ( a ) IV(a) IV(a)得值通常会越大,这就可能导致增益可能对可取数值数目较少的属性有所偏好,因此其在选择分类属性的时候倾向混乱程度更小的属性。
因此可以先计算出信息增益高于平均水平的候选属性,在从中选择增益率最高的
C4.5算法的不足:
- C4.5生成的是多叉树,生成决策树的效率比较慢。
- C4.5只能用于分类。
- C4.5由于使用了嫡模型,里面有大量的耗时的对数运算。
4.2.3 基尼指数( CART算法)
首先看基尼值:从样本集合D中随机抽取两个样本,其类别标记不一致的概率。因此,基尼值越小,这样类别越少,即碰到异类的概率就越小,纯度自然就越高。
Gini
(
D
)
=
∑
k
=
1
∣
Y
∣
∑
k
′
≠
k
p
k
p
k
′
=
p
1
⋅
(
p
2
+
p
3
+
…
+
p
k
)
+
…
+
p
k
⋅
(
p
1
+
p
2
+
p
3
+
…
+
p
k
−
1
)
=
p
1
(
1
−
p
1
)
+
p
2
(
1
−
p
2
)
+
…
+
p
k
(
1
−
p
k
)
=
(
p
1
+
p
2
+
…
+
p
k
)
−
(
p
1
2
+
p
2
2
+
…
+
p
k
2
)
=
∑
k
=
1
∣
Y
∣
p
k
(
1
−
p
k
)
=
1
−
∑
k
=
1
∣
Y
∣
p
k
2
\begin{aligned} \operatorname{Gini}(D) &=\sum_{k=1}^{|\mathcal{Y}|} \sum_{k^{\prime} \neq k} p_{k} p_{k^{\prime}} \\ &=p_{1} \cdot\left(p_{2}+p_{3}+\ldots+p_{k}\right)+\ldots+p_{k} \cdot\left(p_{1}+p_{2}+p_{3}+\ldots+p_{k-1}\right) \\ &=p_{1}\left(1-p_{1}\right)+p_{2}\left(1-p_{2}\right)+\ldots+p_{k}\left(1-p_{k}\right) \\ &=\left(p_{1}+p_{2}+\ldots+p_{k}\right)-\left(p_{1}^{2}+p_{2}^{2}+\ldots+p_{k}^{2}\right) \\ &=\sum_{k=1}^{|\mathcal{Y}|} p_{k}\left(1-p_{k}\right) \\ &=1-\sum_{k=1}^{|\mathcal{Y}|} p_{k}^{2} \end{aligned}
Gini(D)=k=1∑∣Y∣k′=k∑pkpk′=p1⋅(p2+p3+…+pk)+…+pk⋅(p1+p2+p3+…+pk−1)=p1(1−p1)+p2(1−p2)+…+pk(1−pk)=(p1+p2+…+pk)−(p12+p22+…+pk2)=k=1∑∣Y∣pk(1−pk)=1−k=1∑∣Y∣pk2
比如西瓜的色泽有青绿,乌黑,浅白这三个特征,k=1时是青绿,其概率为
p
k
p_k
pk,其他特征的概率就是
1
−
p
k
1-p_k
1−pk,三个特征都选上,再求和就是信息增益。
CART决策树使用“基尼指数”(Gini index)来选择划分属性,基尼指数反映的是从样本集D中随机抽取两个样本,其类别标记不一致的概率,因此Gini(D)越小越好,基尼指数定义如下:
Gini_index
(
D
,
a
)
=
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
Gini
(
D
v
)
(4.6)
\begin{align} \text{Gini\_index}(D,a) & = \sum_{v=1}^V\frac{|D^v|}{|D|}\text{Gini} ({D^v}) \end{align} \tag{4.6}
Gini_index(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)(4.6)
在特征选取中,会优先选择基尼指数最小的属性作为优先划分属性
a
∗
=
arg
min
a
∈
A
Gini_index
(
D
,
a
)
a_* = \underset{a \in A}{\arg\min} \text{Gini\_index}(D,a)
a∗=a∈AargminGini_index(D,a)
**[解析]:**这个是数据集 D D D中属性 a a a的基尼指数的定义,它表示在属性 a a a的取值已知的条件下,数据集 D D D按照属性 a a a的所有可能取值划分后的纯度。
不过在构造CART分类树时并不会严格按照此公式来选择最优划分属性,主要是因为CART分类树是一颗二叉树,如果用上面的公式去选出最优划分属性,无法进一步选出最优划分属性的最优划分点。CART分类树的构造算法如下:
-
首先,对每个属性 a a a的每个可能取值 v v v,将数据集 D D D分为 a = v a=v a=v和 a ≠ v a\neq v a=v两部分来计算基尼指数,即
Gini_index ( D , a ) = ∣ D a = v ∣ ∣ D ∣ Gini ( D a = v ) + ∣ D a ≠ v ∣ ∣ D ∣ Gini ( D a ≠ v ) \operatorname{Gini\_index}(D,a) = \frac{|D^{a=v}|}{|D|}\operatorname{Gini}(D^{a=v})+\frac{|D^{a\neq v}|}{|D|}\operatorname{Gini}(D^{a\neq v}) Gini_index(D,a)=∣D∣∣Da=v∣Gini(Da=v)+∣D∣∣Da=v∣Gini(Da=v) -
然后,选择基尼指数最小的属性及其对应取值作为最优划分属性和最优划分点;
-
最后,重复以上两步,直至满足停止条件。
下面以西瓜书中表4.2中西瓜数据集2.0为例来构造CART分类树,其中第一个最优划分属性和最优划分点的计算过程如下:
以属性“色泽”为例,它有3个可能的取值:
{
青绿,乌黑,浅白
}
\{\text{青绿},\text{乌黑},\text{浅白}\}
{青绿,乌黑,浅白}, 若使用该属性的属性值是否等于“青绿”对数据集
D
D
D进行划分,则可得到2个子集,分别记为
D
1
(
色泽
=
青绿
)
,
D
2
(
色泽
≠
青绿
)
D^1(\text{色泽}=\text{青绿}),D^2(\text{色泽}\not=\text{青绿})
D1(色泽=青绿),D2(色泽=青绿)。子集
D
1
D^1
D1包含编号
{
1
,
4
,
6
,
10
,
13
,
17
}
\{1,4,6,10,13,17\}
{1,4,6,10,13,17}共6个样例,其中正例占
p
1
=
3
6
p_1=\frac{3}{6}
p1=63,反例占
p
2
=
3
6
p_2=\frac{3}{6}
p2=63;子集
D
2
D^2
D2包含编号
{
2
,
3
,
5
,
7
,
8
,
9
,
11
,
12
,
14
,
15
,
16
}
\{2,3,5,7,8,9,11,12,14,15,16\}
{2,3,5,7,8,9,11,12,14,15,16}共11个样例,其中正例占
p
1
=
5
11
p_1=\frac{5}{11}
p1=115,反例占
p
2
=
6
11
p_2=\frac{6}{11}
p2=116,根据公式(4.5)可计算出用“色泽=青绿”划分之后得到基尼指数为
Gini_index
(
D
,
色泽
=
青绿
)
=
6
17
×
(
1
−
(
3
6
)
2
−
(
3
6
)
2
)
+
11
17
×
(
1
−
(
5
11
)
2
−
(
6
11
)
2
)
=
0.497
\operatorname{Gini\_index}(D,\text{色泽}=\text{青绿}) = \frac{6}{17}\times\left(1-(\frac{3}{6})^2-(\frac{3}{6})^2\right)+\frac{11}{17}\times\left(1-(\frac{5}{11})^2-(\frac{6}{11})^2\right) = 0.497
Gini_index(D,色泽=青绿)=176×(1−(63)2−(63)2)+1711×(1−(115)2−(116)2)=0.497
类似的,可以计算出以下不同属性取不同值的基尼指数
Gini_index
(
D
,
色泽
=
乌黑
)
=
6
17
×
(
1
−
(
4
6
)
2
−
(
2
6
)
2
)
+
11
17
×
(
1
−
(
4
11
)
2
−
(
7
11
)
2
)
=
0.456
Gini_index
(
D
,
色泽
=
浅白
)
=
5
17
×
(
1
−
(
1
5
)
2
−
(
4
5
)
2
)
+
12
17
×
(
1
−
(
7
12
)
2
−
(
5
12
)
2
)
=
0.426
\begin{aligned} \operatorname{Gini\_index}(D,\text{色泽}=\text{乌黑}) = \frac{6}{17}\times\left(1-(\frac{4}{6})^2-(\frac{2}{6})^2\right)+\frac{11}{17}\times\left(1-(\frac{4}{11})^2-(\frac{7}{11})^2\right) = 0.456\\ \operatorname{Gini\_index}(D,\text{色泽}=\text{浅白}) = \frac{5}{17}\times\left(1-(\frac{1}{5})^2-(\frac{4}{5})^2\right)+\frac{12}{17}\times\left(1-(\frac{7}{12})^2-(\frac{5}{12})^2\right) = 0.426 \end{aligned}
Gini_index(D,色泽=乌黑)=176×(1−(64)2−(62)2)+1711×(1−(114)2−(117)2)=0.456Gini_index(D,色泽=浅白)=175×(1−(51)2−(54)2)+1712×(1−(127)2−(125)2)=0.426
Gini_index
(
D
,
根蒂
=
蜷缩
)
=
0.456
Gini_index
(
D
,
根蒂
=
稍蜷
)
=
0.496
Gini_index
(
D
,
根蒂
=
硬挺
)
=
0.439
Gini_index
(
D
,
敲声
=
浊响
)
=
0.450
Gini_index
(
D
,
敲声
=
沉闷
)
=
0.494
Gini_index
(
D
,
敲声
=
清脆
)
=
0.439
Gini_index
(
D
,
纹理
=
清晰
)
=
0.286
Gini_index
(
D
,
纹理
=
稍稀
)
=
0.437
Gini_index
(
D
,
纹理
=
模糊
)
=
0.403
Gini_index
(
D
,
脐部
=
凹陷
)
=
0.415
Gini_index
(
D
,
脐部
=
稍凹
)
=
0.497
Gini_index
(
D
,
脐部
=
平坦
)
=
0.362
Gini_index
(
D
,
触感
=
硬挺
)
=
0.494
Gini_index
(
D
,
触感
=
软粘
)
=
0.494
\begin{aligned} \operatorname{Gini\_index}(D,\text{根蒂}=\text{蜷缩}) = 0.456\\ \operatorname{Gini\_index}(D,\text{根蒂}=\text{稍蜷}) = 0.496\\ \operatorname{Gini\_index}(D,\text{根蒂}=\text{硬挺}) = 0.439\\ \operatorname{Gini\_index}(D,\text{敲声}=\text{浊响}) = 0.450\\ \operatorname{Gini\_index}(D,\text{敲声}=\text{沉闷}) = 0.494\\ \operatorname{Gini\_index}(D,\text{敲声}=\text{清脆}) = 0.439\\ \operatorname{Gini\_index}(D,\text{纹理}=\text{清晰}) = 0.286\\ \operatorname{Gini\_index}(D,\text{纹理}=\text{稍稀}) = 0.437\\ \operatorname{Gini\_index}(D,\text{纹理}=\text{模糊}) = 0.403\\ \operatorname{Gini\_index}(D,\text{脐部}=\text{凹陷}) = 0.415\\ \operatorname{Gini\_index}(D,\text{脐部}=\text{稍凹}) = 0.497\\ \operatorname{Gini\_index}(D,\text{脐部}=\text{平坦}) = 0.362\\ \operatorname{Gini\_index}(D,\text{触感}=\text{硬挺}) = 0.494\\ \operatorname{Gini\_index}(D,\text{触感}=\text{软粘}) = 0.494 \end{aligned}
Gini_index(D,根蒂=蜷缩)=0.456Gini_index(D,根蒂=稍蜷)=0.496Gini_index(D,根蒂=硬挺)=0.439Gini_index(D,敲声=浊响)=0.450Gini_index(D,敲声=沉闷)=0.494Gini_index(D,敲声=清脆)=0.439Gini_index(D,纹理=清晰)=0.286Gini_index(D,纹理=稍稀)=0.437Gini_index(D,纹理=模糊)=0.403Gini_index(D,脐部=凹陷)=0.415Gini_index(D,脐部=稍凹)=0.497Gini_index(D,脐部=平坦)=0.362Gini_index(D,触感=硬挺)=0.494Gini_index(D,触感=软粘)=0.494
特别地,对于属性“触感”,由于它的可取值个数为2,所以其实只需计算其中一个取值的基尼指数即可。
根据上面的计算结果可知 Gini_index ( D , 纹理 = 清晰 ) = 0.286 \operatorname{Gini\_index}(D,\text{纹理}=\text{清晰}) = 0.286 Gini_index(D,纹理=清晰)=0.286最小,所以选择属性“纹理”为最优划分属性并生成根节点,接着以“纹理=清晰”为最优划分点生成 D 1 ( 纹理 = 清晰 ) , D 2 ( 纹理 ≠ 清晰 ) D^1(\text{纹理}=\text{清晰}),D^2(\text{纹理}\not=\text{清晰}) D1(纹理=清晰),D2(纹理=清晰)两个子节点,对于两个子节点分别重复上述步骤继续生成下一层子节点,直至满足停止条件。
以上便是CART分类树的构建过程,从构建过程中可以看出,CART分类树最终构造出来的是一颗二叉树。CART决策树除了能处理分类问题以外,它还可以处理回归问题,附录②中给出了CART回归树的构造算法。
基尼系数是一种衡量信息不确定性的方法,与信息熵计算出来的结果差距很小,基本可以忽略,但是基尼系数要计算快得多,因为没有对数
