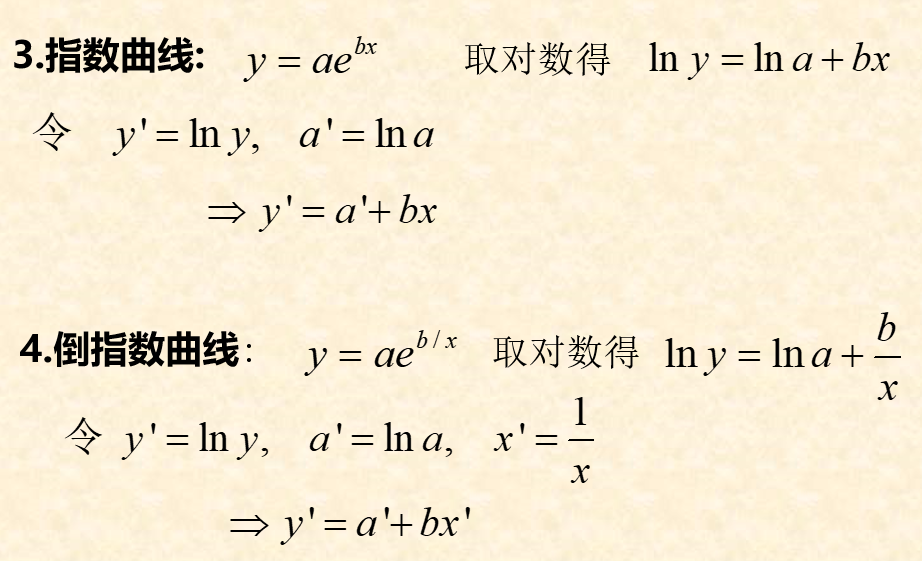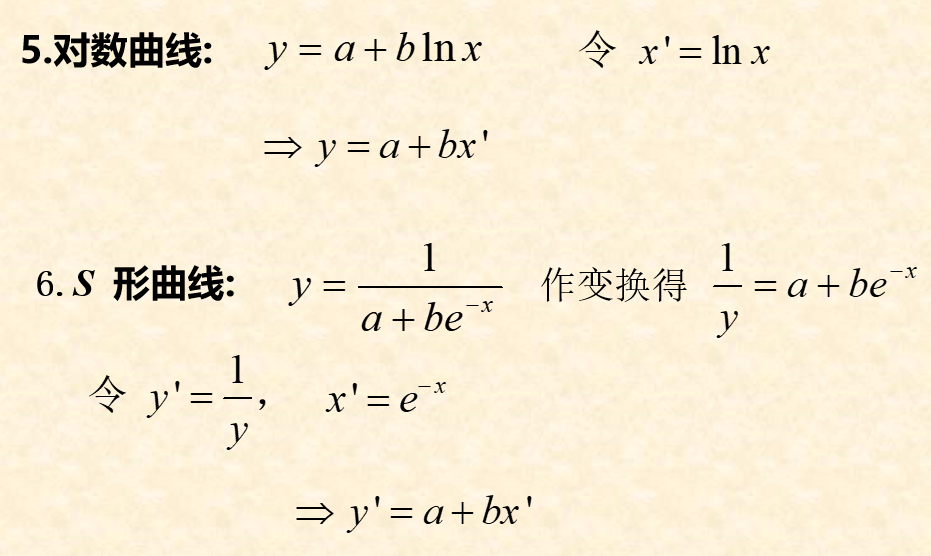当前位置：首页 > news >正文

【概率论与数理统计(研究生课程)】知识点总结9(回归分析)

news 来源：原创 2024/5/19 23:45:56

原文地址：【概率论与数理统计(研究生课程)】知识点总结9(回归分析)

一元线性回归模型

$\begin{aligned} &y=\beta_0+\beta_1x+\epsilon,\quad \epsilon \sim N(\mu, \sigma^2) \\ &E(\epsilon)=0,D(\epsilon)=\sigma^2>0 \Longrightarrow E(y)=\beta_0+\beta_1x \end{aligned}$

回归方程： $\hat{y}=\hat{\beta_0}+\hat{\beta_1}x$

推导过程：
$\begin{aligned} y_i-E(y_i)&=y_i-(\beta_0+\beta_1x_i) \\ Q(\beta_1, \beta_2)&=\sum\limits_{i=1}^{n}(y_i-E(y_i))^2 \\ &=\sum\limits_{i=1}^{n}(y_i-\beta_0-\beta_1x_i)^2 \\ \text{make }\quad\frac{\partial{Q(\beta_0,\beta_1)}}{\partial{\beta_0}}&=-2\sum\limits_{i=1}^{n}(y_i-\beta_0-\beta_1x_i)=0 \\ \text{make }\quad\frac{\partial{Q(\beta_0,\beta_1)}}{\partial{\beta_1}}&=-2\sum\limits_{i=1}^{n}x_i(y_i-\beta_0-\beta_1x_i)=0 \\ \end{aligned}$
整理得到正规方程组：
$\begin{aligned} &n\hat{\beta_0}+n\bar{x}\hat{\beta_1}=n\bar{y}\quad (1)\\ &n\bar{x}\hat{\beta_0}+(\sum\limits^{n}_{i=1}{x_i^2}) \hat{\beta_1} =\sum\limits_{i=1}^{n}x_iy_i \quad (2) \end{aligned}$
解上述方程组得到：
$\begin{aligned} &\hat{\beta_1}=\frac{L_{xy}}{L_{xx}} \\ &\hat{\beta_0}=\bar{y}-\hat{\beta_1}\bar{x} \\ &L_{xx}=\sum\limits_{i=1}^{n}(x_i-\bar{x})^2=\sum\limits_{i=1}^{n}x_i^2-n\bar{x}^2=\sum\limits_{i=1}^{n}x_i^2-\frac{1}{n}(\sum\limits_{i=1}^{n}x_i)^2 \\ &L_{yy}=\sum\limits_{i=1}^{n}(y_i-\bar{y})^2=\sum\limits_{i=1}^{n}y_i^2-n\bar{y}^2=\sum\limits_{i=1}^{n}y_i^2-\frac{1}{n}(\sum\limits_{i=1}^{n}y_i)^2 \\ &L_{xy}=\sum\limits_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})=\sum\limits_{i=1}^{n}x_iy_i-n\bar{x}\bar{y}=\sum\limits_{i=1}^{n}x_iy_i-\frac{1}{n}\sum\limits_{i=1}^{n}x_i \sum\limits_{i=1}^{n}y_i \end{aligned}$

如果题目中给了 $\sum$ 形式的数据， $L_{xx},L_{yy},L_{xy}$ 一般用上述公式最右边的方式来求。

残差/剩余平方和

$Q_e=\sum\limits_{i=1}^{n}e_i^2=\sum\limits_{i=1}^{n}(y_i-\hat{y_i})^2=\sum\limits_{i=1}^{n}(y_i-\hat{\beta_0}-\hat{\beta_1}x_i)^2=L_{yy}-\hat{\beta_1}L_{xy}=L_{yy}-\frac{L_{xy}^2}{L_{xx}}$

定理： $\frac{Q_e}{\sigma^2}\sim\chi^2(n-2)$
$\begin{aligned} &E(\frac{Q_e}{\sigma^2})=n-2 \\ \Longrightarrow \quad &E(\frac{Q_e}{n-2})=\sigma^2 \\ \Longrightarrow \quad &\hat{\sigma^2}=\frac{Q_e}{n-2} \end{aligned}$
$\hat{\sigma}^2$ 的无偏估计为 $\frac{Q_e}{n-2}$

最小二乘估计量的性质

$\beta_0,\beta_1$ 的最小二乘估计量都是无偏的： $E(\hat{\beta_0})=\beta_0,\quad E(\hat{\beta_1})=\beta_1$

$\hat{\beta_0}\sim N(\beta_0, (\frac{1}{n}+\frac{\bar{x}^2}{L_{xx}})\sigma^2)$

$\hat{\beta_1}\sim N(\beta_1,\frac{\sigma^2}{L_{xx}})$

$Cov(\hat{\beta_0},\hat{\beta_1})=-\frac{\bar{x}}{L_{xx}}\sigma^2$

$\hat{y_0}\sim N(\beta_0+\beta_1x_0, (\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}})\sigma^2)$

回归方程显著性检验（t、F、r）

提出原假设和备择假设（回归方程是否显著，反映在斜率是否为0）：

$H_0: \beta_1=0; \quad H_1:\beta_1\neq0$

选取统计量：
$\begin{aligned} &\hat{\beta_1}\sim N(\beta_1,\frac{\sigma^2}{L_{xx}}) \\ \Longrightarrow \quad &\frac{\hat{\beta_1}-\beta_1}{\sqrt{\frac{\sigma^2}{L_{xx}}}}\sim N(0,1) \\ \xrightarrow{H_0} \quad &\frac{\hat{\beta_1}\sqrt{L_{xx}}}{\sigma}\sim N(0,1) \end{aligned}$
若需构造 $t$ 检验，还需要一个 $\chi^2$ 分布，而 $\frac{Q_e}{\sigma^2}\sim\chi^2(n-2)$ ，从而：
$T=\frac{\frac{\hat{\beta_1}\sqrt{L_{xx}}}{\sigma}}{\sqrt{\frac{Q_e}{\sigma^2}/(n-2)}}\xrightarrow{\hat{\sigma^2}=\frac{Q_e}{n-2}}\frac{\hat{\beta_1}\sqrt{L_{xx}}}{\hat\sigma} \sim t(n-2)$
若使用 $F$ 检验，需要计算回归平方和以及残差平方和：
$\begin{aligned} &S_R^2=\sum\limits_{i=1}^{n}(\hat{y_i}-\bar{y_i})^2=\hat{\beta_1}L_{xy} \\ &S_e^2=\sum\limits_{i=1}^{n}(y_i-\hat{y_i})^2=S_T^2-S_R^2=L_{yy}-\hat{\beta_1}L_{xy} \\ &\frac{S_R^2}{\sigma^2}\sim \chi^2(1), \quad \frac{S_e^2}{\sigma^2}\sim \chi^2(n-2) \\ &F=\frac{\frac{S_R^2}{\sigma^2}/1}{\frac{S_e^2}{\sigma^2}/(n-2)}=\frac{(n-2)S_R^2}{S_e^2}\sim F(1,n-2) \end{aligned}$
拒绝域

$t$ 检验拒绝域： $|T|=|\frac{\hat{\beta_1}\sqrt{L_{xx}}}{\hat{\sigma}}|\ge t_{\frac{\alpha}{2}}(n-2)$

$F$ 检验拒绝域： $F\ge F_\alpha(1,n-2)$
确定 $t_{\frac{\alpha}{2}(n-2)}\quad or \quad F_{\alpha}(1,n-2)$
计算 $|T|\quad or\quad F$
判断结果

回归系数的区间估计

$\begin{aligned} &\hat{\beta_1}\sim N(\beta_1,\frac{\sigma^2}{L_{xx}}) \\ \Longrightarrow \quad &\frac{\hat{\beta_1}-\beta_1}{\sqrt{\frac{\sigma^2}{L_{xx}}}}\sim N(0,1) \\ \Longrightarrow \quad &\frac{(\hat{\beta_1}-\beta_1)\sqrt{L_{xx}}}{\sigma}\sim N(0,1) \\ T=\frac{\frac{(\hat{\beta_1}-\beta_1)\sqrt{L_{xx}}}{\sigma}}{\sqrt{\frac{Q_e}{\sigma^2}/(n-2)}}&\xrightarrow{\hat{\sigma^2}=\frac{Q_e}{n-2}}\frac{(\hat{\beta_1}-\beta_1)\sqrt{L_{xx}}}{\hat\sigma} \sim t(n-2) \end{aligned}$

则 $\beta_1$ 置信水平为 $1-\alpha$ 的置信区间为： $(\hat{\beta_1}\pm \frac{\hat{\sigma}}{\sqrt{L_{xx}}}t_{\frac{\alpha}{2}}(n-2))$

单值预测

设回归方程为 $\hat{y}=\hat{\beta_0}+\hat{\beta_1}x$ ，对任意给定的 $x=x_0$ ， $y_0$ 的预测值为 $\hat{y_0}=\hat{\beta_0}+\hat{\beta_1}x_0$

$\hat{\beta_0}\sim N(\beta_0, (\frac{1}{n}+\frac{\bar{x}^2}{L_{xx}})\sigma^2)$

$\hat{\beta_1}\sim N(\beta_1,\frac{\sigma^2}{L_{xx}})$

$Cov(\hat{\beta_0},\hat{\beta_1})=-\frac{\bar{x}}{L_{xx}}\sigma^2$

$D(\hat{y_0})=D(\hat{\beta_0})+D(\hat{\beta_1}x_0)+2Cov(\hat{\beta_0,\hat{\beta_1}x_0})=(\frac{1}{n}+\frac{(\bar{x}-x_0)^2}{L_{xx}})\sigma^2$

$\hat{y_0}\sim N(\beta_0+\beta_1x_0, (\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}})\sigma^2)$

区间预测

$\begin{aligned} y_0-\hat{y_0}\sim N(0,[1+\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}}]\sigma^2) \\ U=\frac{y_0-\hat{y_0}}{\sigma\sqrt{1+\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}}}}\sim N(0,1) \\ T=\frac{y_0-\hat{y_0}}{\hat\sigma\sqrt{1+\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}}}}\sim t(n-2) \end{aligned}$

因此， $y_0$ 的置信度为 $1-\alpha$ 的区间为 $(\hat{y_0}-\delta,\hat{y_0}+\delta),\delta=t_{\frac{\alpha}{2}}(n-2)\hat{\sigma}\sqrt{1+\frac{1}{n}+\frac{(x_0-\bar{x})^2}{L_{xx}}}$