出处:https://blog.csdn.net/wuaini_1314/article/details/79562400
线性最小二乘问题,我们可以通过理论推导可以得到其解析解,但是对于非线性最小二乘问题,则需要依赖迭代优化的方法,。
梯度下降主要是从一阶目标函数的一阶导推导而来的,形象点说,就是每次朝着当前梯度最大的方向收敛;二牛顿法是二阶收敛,每次考虑收敛方向的时候,还会考虑下一次的收敛的方向是否是最大(也就是梯度的梯度)。可以参考下图:
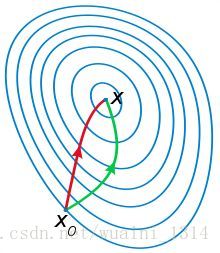
红线为牛顿法,绿线为梯度下降。
高斯-牛顿和LM法则主要是针对非线性最小二乘问题提出的解决方案。由于牛顿法需要求解二阶导,也就是hessian matrix,运算量大,不利于实现,,所以通常在牛顿法的基础上用去掉二阶项,用一阶项来近似二阶导,从而保证了计算效率。LM方法,则是由于高斯-牛顿方法在计算时需要保证矩阵的正定性,于是引入了一个约束,从而保证计算方法更具普适性。
1.梯度下降与牛顿法[2]
梯度下降法:
梯度是上升最快的方向,那么如果我想下山,下降最快的方向呢,当然是逆着梯度了(将一点附近的曲面近似为平面),这就是梯度下降法,由于是逆着梯度,下降最快,又叫最速下降法。(一句话就是,朝着梯度方向收敛,可以参考梯度的定义)
迭代公式:
b=a−γ∇F(a)b=a−γ∇F(a) ,γγ是步长。
牛顿法:
最优化问题中,牛顿法首先则是将问题转化为求 f‘(x) = 0 这个方程的根。
首先得到一个初始解 x0,
一阶展开:f′(x)≈f‘(x0)+(x-x0)f″(x0)f′(x)≈f‘(x0)+(x-x0)f″(x0)
令f‘(x0)+(x-x0)f″(x0)=0f‘(x0)+(x-x0)f″(x0)=0
求解得到x,相比于x0,f‘(x)<f′(x0)f‘(x)<f′(x0)
总结一下
其实我们不知道函数的极值点(一阶导的0解),但是我们不知道这个函数是什么样的
但是我们知道每个点的函数
所以,梯度法就是直接求导然后朝着这个点下降最快的方向走一步
牛顿法是用这个点二阶导去近似这个函数的一阶导,然后求0解
优缺点:
梯度法:又称最速下降法,是早期的解析法,收敛速度较慢。
牛顿法:收敛速度快,但不稳定,计算也较困难。
2.高斯牛顿和LM方法
推导过程可以参考
http://blog.csdn.net/zhubaohua_bupt/article/details/74973347
http://fourier.eng.hmc.edu/e176/lectures/NM/node36.html
http://blog.csdn.net/dsbatigol/article/details/12448627
需要注意的是 高斯牛顿方法 在求解hessian matrix时 做了一个简化
目标函数可以简写:
S=∑mi=1r2iS=∑i=1mri2
梯度向量在方向上的分量:
gj=2∑mi=1ri∂ri∂βjgj=2∑i=1mri∂ri∂βj (1)
Hessian 矩阵的元素则直接在梯度向量的基础上求导:
Hjk=2∑mi=1(∂ri∂βj∂ri∂βk+ri∂2ri∂βj∂βk).Hjk=2∑i=1m(∂ri∂βj∂ri∂βk+ri∂2ri∂βj∂βk).
高斯牛顿法的一个小技巧是,将二次偏导省略,于是:
Hjk≈2∑mi=1JijJikHjk≈2∑i=1mJijJik (2)
将(1)(2)改写成 矩阵相乘形式:
g=2Jr⊤r,H≈2Jr⊤Jr.g=2Jr⊤r,H≈2Jr⊤Jr.
Levenberg-Marquardt方法:
高斯-牛顿法中为了避免发散,有两种解决方法
1.调整下降步伐:βs+1=βs+α Δ.0<α<1βs+1=βs+α Δ.0<α<1
2.调整下降方向:(JTJ+λD)Δ=JTr(JTJ+λD)Δ=JTr
λ→+∞λ→+∞时:Δ/λ→JTrΔ/λ→JTr,即方向和梯度方向一样,变成了梯度下降法。
相反,如果λ为0,就变成了高斯牛顿法。
Levenberg-Marquardt方法的好处在于可以调节:
如果下降太快,使用较小的λ,使之更接近高斯牛顿法
如果下降太慢,使用较大的λ,使之更接近梯度下降法
此外,高斯牛顿法中涉及求逆矩阵的操作,(JTJ)(JTJ) 加入λ 也可以保证该矩阵为一个正定矩阵。
【reference】:
[1]http://fourier.eng.hmc.edu/e176/lectures/NM/node36.html 【理论推导很完善】
[2].http://blog.csdn.net/dsbatigol/article/details/12448627
有关梯度下降法:
http://www.cnblogs.com/shixiangwan/p/7532858.html
https://www.zhihu.com/question/19723347
http://www.cnblogs.com/maybe2030/p/5089753.html
梯度下降与牛顿法:
https://www.cnblogs.com/shixiangwan/p/7532830.html
