1.统计子矩阵

1.问题描述

小明有一个大小为 $N\times M$ 的矩阵，可以理解为一个 $N$ 行 $M$ 列的二维数组。我们定义一个矩阵 $m$ 的稳定度 $f(m)$ 为 $f(m)=max(m)-min(m)$，其中 $max(m)$
表示矩阵 $m$ 中的最大值，$min(m)$ 表示矩阵 $m$ 中的最小值。现在小明想要从这个矩阵中找到一个稳定度不大于 $limit$ 的子矩阵，同时他还希望这个子矩阵的面积越大越好（面积可以理解为矩阵中元素个数）。
子矩阵定义如下：从原矩阵中选择一组连续的行和一组连续的列，这些行列交点上的元素组成的矩阵即为一个子矩阵。

2.输入格式

  第一行输入两个整数 $N，M$，表示矩阵的大小。
  接下来 $N$ 行，每行输入 $M$ 个整数，表示这个矩阵。
  最后一行输入一个整数 $limit$，表示限制。

3.输出格式

  输出一个整数，分别表示小明选择的子矩阵的最大面积。

4.样例输入

3 4
2 0 7 9
0 6 9 7
8 4 6 4
8

5.样例输出

6

6.数据范围

$1\le n\le 80，1\le m\le 10^5，1\le n\ast m\le 10^5$
$0\le$ 矩阵元素值，$limit\le 10^5$

7.原题链接

统计子矩阵

2.解题思路

• $(1)$题意比较简单，确定一个矩阵，只需要确定左上端点和右下端点，自然而然想到一个最朴素最暴力想法——去枚举两个端点。很显然这样的复杂度是$O(n^2{m}^2\beta (t))$，其中$\beta (t)$是判断每个矩阵所需要的时间，设该矩阵的长为 $x$，宽为 $y$ ，则$\beta (t)=x\ast y$。但很明显这样的思路是超时的，光是 $m^2$ 的复杂度就是我们无法接受的。
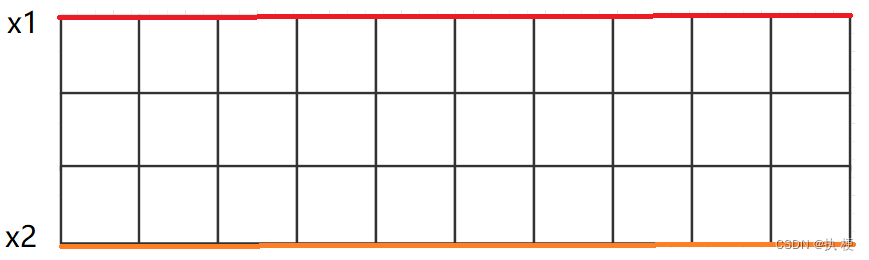
• $(2)$假设一个矩阵的左上端点的坐标为$(x_1,y_1)$，右下坐标的端点为$(x_2，y_2)$。仔细观察数据范围可以发现，$n$ 非常小，这意味着我们可以暴力枚举两点的横坐标 $x_1$ 和 $x_2$，这样做的复杂度为 $n^2$。这样处理后，意味着我们只需要在这个下图中的红轴和橙轴各找到一个点，也就是找到 $y1$ 和 $y2$ ,使得矩阵的稳定度是不大于$limit$，我们先不考虑如何枚举$y1$和$y2$这个问题，先考虑对于一个确定的矩阵，如何高效的算出它的$\beta (t)$。
  
• $(3)$对于一个矩阵，并没有一个高效求出它的 $max$以及 $min$的算法 ,但如果是一个一维数组，求区间的最值就有许多方法，比如$st$表，线段树、单调队列等。我们不禁去思考，能否将一个二维矩阵处理为一维？
  显然这是可行的！
  假设对于一个下面的二维矩阵，设宽为 $y$，高为 $x$ ，暴力求最值的复杂度是$O(xy)$
  
  如果我们可以先处理得到每一列的最值，并将其放到该列的末尾，那么对于该矩阵的最值，我们只需要考虑最后一行即可。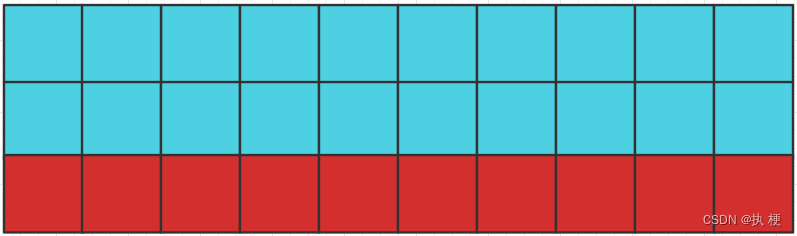
  如图每个红色都格子都是该列的最值$(max/min)$，那么当我们需要求解该矩阵的最大值或者最小值时，复杂度都将只和矩阵的宽度有关，时间复杂度将会是$O(y)$。
  $(4)$当然如何预处理是一个关键，我们生成两个数组$max[k][i][j]$以及$min[k][i][j]$，其中$max[k][i][j]$代表的含义是在第$k$列中，第 $i$ 个元素到第 $j$ 个的元素最大值是多少，$min$数组同理。我们预处理的转移式子应该为：
  $$max[k][i][j]=max(max[k][i][j-1],max[k][j][j]);$$
  这个式子的含义也很简单，对于区间$[i,j]$的最大值应该是$[i,j-1]$的最大值和 $j$ 位值取较大值。
  由于我们处理的是每一列，这样时间复杂度是$O(n^2)$，由于总共有$m$，所以总时间复杂度应该是$O(n^{2}m)$，这是完全可接受的。这样我们就完成了这道题第一个难点的跨越。
  这一步的操作可以这样理解：
    有一个部落，它有$m$个村庄，每次村庄都有$n$个人，每次我们需要去找到一堆村庄内最强的那个人，如果每次计算最坏都有可能是$O(nm)$的复杂度，那么不如先让每个村庄自己内部打一架，派出一个最强代表，每次我们只需要让代表打一架就好了，这样复杂度就只是$O(m)$
• $(5)$现在让我们再回到之前的一个问题，确定了$x1$和$x2$的情况下，如何去确定$y1$和$y2$呢，如果同样暴力枚举的话复杂度是$O(m^2)$不可接受。在这里我们可以巧妙地进行二分答案。因为本质上横坐标$x$确定的是矩阵高，而$y$确定的是矩阵的宽，我们去二分宽度——矩阵内是否存在宽度为 $l$ 的矩阵稳定度不大于$limit$。
• $(6)$既然可以二分，那就一定要分析其是否具有二段性，明显是有的。如果存在一个宽度为 $l$ 的矩阵符合要求，那么一定能找到一个宽度在区间$[1,l-1]$的矩阵也符合要求。这也非常好证明：对于下图
  
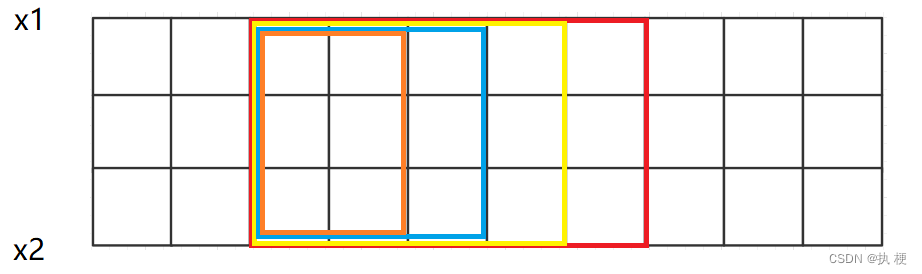
  假设红色矩阵的值域为$[l,r]$，且$r-l<=limit$，说明该矩阵是稳定矩阵。因为橙色、蓝色、黄色矩阵都是红色的子矩阵，说明它的值域一定也是在$[l,r]$，那么说明它们也一定是稳定矩阵，到此可以说明二分的正确性。本题的第二个难点就此解决。
• $(7)$当然既然二分当然要说明 $check$ 函数的逻辑，当二分的值为$mid$时，也就是需要去判断是否存在宽度为$mid$的矩阵符合要求，因为我们前面预处理已经将高度压缩为1，所以这其实就是一个一维数组滑动窗口求最值问题，属于是单调队列的模板使用，求出每个长度为$mid$的窗口的最大值$max$和最小值$min$，只要有一个窗口符合$max-min<=limit$我们都返回true，否则返回false。
• $(8)$当二分得到最长宽度为 $r$ 时，该矩阵的面积就为$(x2-x1+1)\ast r$，每次用一个全局变量更新答案。考虑时间复杂度——枚举横坐标为$O(n^2)$，二分的复杂度为$O(logm)$，每次$check$判定的复杂度是$O(m)$，所以整体时间复杂度为$O(n^{2}mlogm)$。

3.Ac_code

import java.io.*;
import java.util.*;

public class 统计子矩阵 {
    //max[k][i][j]表示第k列中[i,j]之间的最大值
    static int[][][] max;
    static int[][][] min;
    static int n, m, limit,ans;
    static BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
    static PrintWriter out=new PrintWriter(new OutputStreamWriter(System.out));
    public static void main(String[] args) throws IOException {
        String[] s=br.readLine().split(" ");
        n = Integer.parseInt(s[0]);
        m = Integer.parseInt(s[1]);
        max=new int[m+1][n+1][n+1];
        min=new int[m+1][n+1][n+1];
        for (int i = 1; i <= n; i++) {
            s=br.readLine().split(" ");
            for (int j = 1; j <= m; j++) {
                max[j][i][i] = min[j][i][i] = Integer.parseInt(s[j-1]);
            }
        }
        limit = Integer.parseInt(br.readLine());
        //预处理  复杂度 n^2*m
        for (int k = 1; k <= m; ++k) {
            for (int i = 1; i <= n; ++i) {
                for (int j = i + 1; j <= n; ++j) {
                    max[k][i][j] = Math.max(max[k][i][j - 1], max[k][j][j]);
                    min[k][i][j] = Math.min(min[k][i][j - 1], min[k][j][j]);
                }
            }
        }
        for (int x1 = 1; x1 <= n; x1++) {
            for (int x2 = x1; x2 <= n; x2++) {
                int l = 1, r = m;
                while (l < r) {
                    int mid = l + r + 1 >> 1;
                    if (check(x1, x2, mid)) l = mid;
                    else r = mid - 1;
                }
                if (check(x1,x2,r)) ans=Math.max(ans,(x2-x1+1)*r);
            }
        }
        out.println(ans);
        out.flush();
    }

    //k是窗口大小
    static boolean check(int x1, int x2, int k) {
        Deque<Integer> qmax = new ArrayDeque<>();
        Deque<Integer> qmin = new ArrayDeque<>();
        for (int i = 1; i <= m; i++) {
            //处理最小
            if (!qmin.isEmpty() && qmin.peekFirst() < i - k + 1) qmin.pollFirst();
            while (!qmin.isEmpty() && min[qmin.peekLast()][x1][x2] > min[i][x1][x2]) qmin.pollLast();
            qmin.offerLast(i);
            //处理最大
            if (!qmax.isEmpty() && qmax.peekFirst() < i - k + 1) qmax.pollFirst();
            while (!qmax.isEmpty() && max[qmax.peekLast()][x1][x2] < max[i][x1][x2]) qmax.pollLast();
            qmax.offerLast(i);
            //说明窗口为k
            if (i >= k && max[qmax.peekFirst()][x1][x2] - min[qmin.peekFirst()][x1][x2] <= limit) return true;
        }
        return false;
    }
}