西瓜书研读——第五章 神经网络:感知机与多层网络
西瓜书研读系列:
西瓜书研读——第三章 线性模型:一元线性回归
西瓜书研读——第三章 线性模型:多元线性回归
西瓜书研读——第三章 线性模型:线性几率回归(逻辑回归)
西瓜书研读——第三章 线性模型: 线性判别分析 LDA
西瓜书研读——第四章 决策树:ID3、C4.2、CSRT算法
- 主要教材为西瓜书,结合南瓜书,统计学习方法,B站视频整理~
- 人群定位:学过高数会求偏导、线代会矩阵运算、概率论知道啥是概率
- 原理讲解,公式推导,课后习题,实践代码应有尽有,欢迎订阅
5.1 神经元模型
所谓神经网络,目前用得最广泛的一个定义是“神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所做出的交互反应”。
M-P神经元
M-P神经元:接收n个输入(通常是来自其他神经元),并给各个输入赋予权重计算加权和,然后和自身特有的阈值θ进行比较(作减法),最后经过激活函数f(模拟“抑制"和“激活”)处理得到输出(通常是给下一个神经元)
M-P神经元模型如下图所示:

y
=
f
(
∑
i
=
1
n
w
i
x
i
−
θ
)
=
f
(
w
T
x
+
b
)
y=f(\sum_{i=1}^nw_ix_i-θ)=f(w^Tx+b)
y=f(i=1∑nwixi−θ)=f(wTx+b)
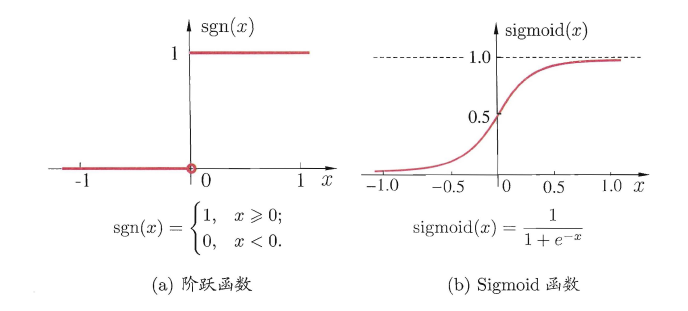
与线性分类十分相似,神经元模型最理想的激活函数也是阶跃函数,即将神经元输入值与阈值的差值映射为输出值1或0,若差值大于零输出1,对应兴奋;若差值小于零则输出0,对应抑制。
但阶跃函数不连续,不光滑,故在M-P神经元模型中,也采用Sigmoid函数来近似, Sigmoid函数将较大范围内变化的输入值挤压到 (0,1) 输出值范围内,所以也称为挤压函数(squashing function)。
常见激活函数f:
- sgn函数
- sigmoid函数
将多个神经元按一定的层次结构连接起来,就得到了神经网络。它是一种包含多个参数的模型,比方说10个神经元两两连接,则有100个参数需要学习(每个神经元有9个连接权以及1个阈值),若将每个神经元都看作一个函数,则整个神经网络就是由这些函数相互嵌套而成。
5.2 感知机与多层网络
感知机模型
感知机(Perceptron)是由两层神经元组成的一个简单模型,但只有输出层是M-P神经元,即只有输出层神经元进行激活函数处理,也称为功能神经元;输入层只是接受外界信号(样本属性)并传递给输出层(输入层的神经元个数等于样本的属性数目),而没有激活函数。
激活函数为sgn (阶跃函数)的神经元
y
=
s
g
n
(
w
T
x
−
θ
)
=
{
1
,
w
T
x
−
θ
⩾
0
0
,
w
T
x
−
θ
<
0
y=sgn(w^Tx-θ)= \left\{\begin{array} {ll} 1, & \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}-\theta \geqslant 0 \\ 0, & \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}-\theta<0 \end{array}\right.
y=sgn(wTx−θ)={1,0,wTx−θ⩾0wTx−θ<0
x为特征向量,作为模型输入,(w,θ)$为神经元参数(权重,阈值)
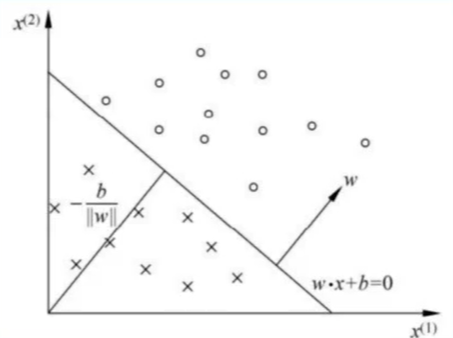
感知机的几何解释:
线性方程
w
T
x
+
b
=
0
\boldsymbol{w}^{T} \boldsymbol{x}+b=0
wTx+b=0对应于特征空间(输入空间)
R
n
R^{n}
Rn 中的一个超平面S,其中
w
\boldsymbol{w}
w是超 平面的法向量,$\mathrm{b} $是超平面的截距。这个超平面将特征空间划分为两个部分。位于两边的点 (特征向量) 分别被分为正、负两类。因此,超平面S称为分离超平面,如图所示:
感知机学习策略
假设训练数据集是线性可分的,感知机学习的目标是求得一个能够将训练集正实例点和负实 例点完全正确分开的超平面。为了找出这样的超平面 S S S,即确定感知机模型参数 w \boldsymbol{w} w 和 b \mathrm{b} b,需要确定一个学习策略,即定义损失函数并将损失函数极小化。损失函数的一个自然选择是误分类点的总数。但是,这样的损失函数不是参数 w \boldsymbol{w} w 和 b b b 的连续可导函数,不易优化,所以感知机采用的损失函数为误分类点到超平面的总距离。
输入空间 R n R^{n} Rn 中点 x 0 \boldsymbol{x}_{0} x0 到超平面 S \mathrm{S} S的距离公式为
∣ w T x 0 + b ∣ ∥ w ∥ \frac{\left|\boldsymbol{w}^{T} \boldsymbol{x}_{0}+b\right|}{\|\boldsymbol{w}\|} ∥w∥∣ ∣wTx0+b∣ ∣
其中,
∥
w
∥
\|\boldsymbol{w}\|
∥w∥ 表示向量 $ \boldsymbol{w} $ 的
L
2
L_{2}
L2范数,也即模长。若将b看成哑结点,也即合并进w可得:
∣
w
^
T
x
^
0
∣
∥
w
∥
\frac{\left|\boldsymbol{\hat w}^{T} \boldsymbol{\hat x}_{0}\right|}{\|\boldsymbol{w}\|}
∥w∥∣
∣w^Tx^0∣
∣
设吴分类点集合为M,那么所有误分类点到超平面S的总距离为
∑
x
^
i
∈
M
∣
w
^
T
x
^
i
∣
∥
w
^
∥
\sum_{\hat{\boldsymbol{x}}_{i} \in M} \frac{\left|\hat{\boldsymbol{w}}^{T} \hat{\boldsymbol{x}}_{i}\right|}{\|\hat{\boldsymbol{w}}\|}
x^i∈M∑∥w^∥∣
∣w^Tx^i∣
∣
随机初始化w, b,将全体训练样本代入模型找出误分类样本,假设此时误分类样本集合为
M
∈
T
M∈T
M∈T,对任意一个误分类样本来说,以下公式恒成立:
(
y
^
−
y
)
(
w
^
T
x
^
−
θ
)
>
=
0
(\hat{y}-y)(\hat w^T\hat x-θ)>=0
(y^−y)(w^Tx^−θ)>=0
y
^
\hat y
y^是预测值,
- 若y是原来是1,预测成了0,即 y ^ = 0 \hat y=0 y^=0,$ 0-1<0 , , ,(w^Tx-θ)=0$
- 若y是原来是0,预测成了1,即 y ^ = 1 \hat y=1 y^=1,$ 1-0>0 , , ,(w^Tx-θ)=1$
所以,给定数据集T,其损失函数可以定义为:
L
(
w
,
θ
)
=
∑
x
∈
M
(
y
^
−
y
)
(
w
T
x
−
θ
)
L(w,θ)=\sum_{x∈M}(\hat{y}-y)(w^Tx-θ)
L(w,θ)=x∈M∑(y^−y)(wTx−θ)
其中, $\hat{y}_{i} $为当前感知机的输出。于是所有误分类点到超平面S的总距离可改写为
∑
x
^
i
∈
M
(
y
^
i
−
y
i
)
w
^
T
x
^
i
∥
w
^
∥
\sum_{\hat{\boldsymbol{x}}_{i} \in M} \frac{\left(\hat{y}_{i}-y_{i}\right) \hat{\boldsymbol{w}}^{T} \hat{\boldsymbol{x}}_{i}}{\|\hat{\boldsymbol{w}}\|}
x^i∈M∑∥w^∥(y^i−yi)w^Tx^i
不考虑
1
∥
w
^
∥
\frac{1}{\|\hat{\boldsymbol{w}}\|}
∥w^∥1 就得到感知机学习的损失函数
L
(
w
^
)
=
∑
x
^
i
∈
M
(
y
^
i
−
y
i
)
w
^
T
x
^
i
L(\hat{\boldsymbol{w}})=\sum_{\hat{\boldsymbol{x}}_{i} \in M}\left(\hat{y}_{i}-y_{i}\right) \hat{\boldsymbol{w}}^{T} \hat{\boldsymbol{x}}_{i}
L(w^)=x^i∈M∑(y^i−yi)w^Tx^i
显然,损失函数 $ L(\hat{\boldsymbol{w}}) $是非负的。如果没有误分类点,损失函数值是 0 。而且,误分类点越 少,误分类点离超平面越近,损失函数值就越小,在误分类时是参数 $ \hat{w} $的线性函数,在正确分类时是0。因此,给定训练数据集,损失函数 $L(\hat{\boldsymbol{w}}) $是 $ \hat{\boldsymbol{w}} $的连续可导函数。
具体地,给定数据集
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
n
,
y
n
)
}
T = \{(x_1, y_1), (x_2,y_2),...,(x_n,y_n)\}
T={(x1,y1),(x2,y2),...,(xn,yn)}
其中
x
i
∈
R
,
y
i
∈
{
0
,
1
}
x_i∈R,y_i∈\{0,1\}
xi∈R,yi∈{0,1},求参数
w
,
θ
,
w,θ,
w,θ,使其为极小化损失函数的解:
m
i
n
L
(
w
,
θ
)
=
m
i
n
w
,
θ
∑
x
i
∈
M
(
y
i
^
−
y
i
)
w
^
T
x
^
i
min\, L(w,θ)= {min}_{w,θ}\sum_{x_i∈M}(\hat{y_i}- y_i)\hat{\boldsymbol{w}}^{T} \hat{\boldsymbol{x}}_{i}
minL(w,θ)=minw,θxi∈M∑(yi^−yi)w^Tx^i
求解
感知机学习算法是误分类驱动的,具体采用随机梯度下降法。首先,任意选取一个超平面 w ^ 0 T x ^ = 0 \hat{\boldsymbol{w}}_{0}^{T} \hat{\boldsymbol{x}}=0 w^0Tx^=0用梯度下降法不断地极小化损失函数$ L(\hat{\boldsymbol{w}})$,极小化过程中不是一次使M中所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下降。已知损失函数的梯度为
∇
L
(
w
^
)
=
∂
L
(
w
^
)
∂
w
^
=
∂
∂
w
^
[
∑
x
^
i
∈
M
(
y
^
i
−
y
i
)
w
^
T
x
^
i
]
=
∑
x
^
i
∈
M
[
(
y
^
i
−
y
i
)
∂
∂
w
^
(
w
^
T
x
^
i
)
]
\nabla L(\hat{\boldsymbol{w}})=\frac{\partial L(\hat{\boldsymbol{w}})}{\partial \hat{\boldsymbol{w}}}=\frac{\partial}{\partial \hat{\boldsymbol{w}}}\left[\sum_{\hat{\boldsymbol{x}}_{i} \in M}\left(\hat{y}_{i}-y_{i}\right) \hat{\boldsymbol{w}}^{T} \hat{\boldsymbol{x}}_{i}\right]\\ =\sum_{\hat{\boldsymbol{x}}_{i} \in M}\left[\left(\hat{y}_{i}-y_{i}\right) \frac{\partial}{\partial \hat{\boldsymbol{w}}}\left(\hat{\boldsymbol{w}}^{T} \hat{\boldsymbol{x}}_{i}\right)\right]
∇L(w^)=∂w^∂L(w^)=∂w^∂[x^i∈M∑(y^i−yi)w^Tx^i]=x^i∈M∑[(y^i−yi)∂w^∂(w^Tx^i)]
由矩阵微分公式
∂
x
T
a
∂
x
=
a
\frac{\partial \boldsymbol{x}^{T} a}{\partial x}=\boldsymbol{a}
∂x∂xTa=a可得
∇
L
(
w
^
)
=
∂
L
(
w
^
)
∂
w
^
=
∑
x
^
i
∈
M
(
y
^
i
−
y
i
)
x
^
{\nabla L(\hat{\boldsymbol{w}})}=\frac{\partial L(\hat{\boldsymbol{w}})}{\partial \hat{\boldsymbol{w}}}=\sum_{\hat{\boldsymbol{x}}_{i} \in M}\left(\hat{y}_{i}-y_{i}\right) \hat{\boldsymbol{x}}
∇L(w^)=∂w^∂L(w^)=x^i∈M∑(y^i−yi)x^
感知机的学习算法具体采用的是随机梯度下降法,也就是极小化过程中不是一次使M中所有误分类点的梯度下降,而是随机选取一个误分类点使其梯度下降。所以权重w的更新公式为:(η为学习率)
w
^
=
w
^
+
△
w
^
\hat w=\hat w+△\hat w
w^=w^+△w^
△ w = − η ∇ L ( w ^ ) △w=-η \nabla L(\hat w) △w=−η∇L(w^)
w ^ ← w ^ − η ∇ L ( w ^ ) w ^ ← w ^ − η ( y ^ i − y i ) x ^ i = w ^ + η ( y i − y ^ i ) x ^ i \begin{array}{c} \hat{\boldsymbol{w}} \leftarrow \hat{\boldsymbol{w}}-\eta \nabla L(\hat{\boldsymbol{w}}) \\ \hat{\boldsymbol{w}} \leftarrow \hat{\boldsymbol{w}}-\eta\left(\hat{y}_{i}-y_{i}\right) \hat{\boldsymbol{x}}_{i}=\hat{\boldsymbol{w}}+\eta\left(y_{i}-\hat{y}_{i}\right) \hat{\boldsymbol{x}}_{i} \end{array} w^←w^−η∇L(w^)w^←w^−η(y^i−yi)x^i=w^+η(yi−y^i)x^i
前馈网络
由于像感知机这种单个神经元分类能力有限, 只能分类线性可分的数据集,对于线性不可分的数据集则无能为力, 但是多个神经元构成的神经网络能够分类线性不可分的数据集(西瓜书上异或问题的那个例子),且有理论证明(通用近似定理):只需一个包含足够多神经元的隐层, 多层前馈网络(最经典的神经网络之一)就能以任意精度逼近任意复杂度的连续函数。
因此, 神经网络既能做回归, 也能做分类, 而且不需要复杂的特征工程。
要解决非线性可分问题,需考虑使用多层功能神经元.例如下图中这个简单的两层感知机就能解决异或问题.在下图a中,输出层与输入层之间的一层神经元,被称为隐层或隐含层,隐含层和输出层神经元都是拥有激活函数的功能神经元.
更一般的,常见的神经网络是形如下图所示的层级结构,每层神经元与下一层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接.这样的神经网络结构通常称为“多层前馈神经网络”
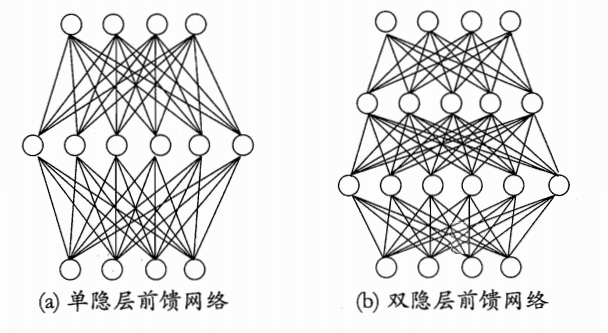
其中输入层神经元仅是接受输入,不进行函数处理,隐层与输出层包含功能神经元."连接权"以及每个功能神经元的阈值;神经网络“学”到的东西,蕴涵在连接权与阈值中.
