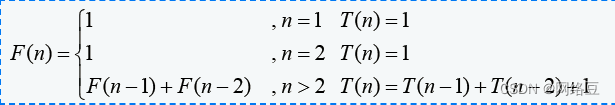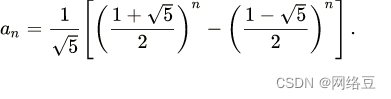初入算法(2)—— 进入算法世界
14天阅读挑战赛
作者简介:一名在校计算机学生、每天分享学习经验、和学习笔记。
座右铭:低头赶路,敬事如仪
点赞,收藏,评论,支持一下博主~ 谢谢~~
目录
前言
一.爆炸增量函数
1.引入故事:《一棋盘的麦子》
2.算法中的时间复杂度
3.常见的时间复杂度类型
二.兔子数列
1.什么是兔子数列
2.递推公式
3.尾数循环
前言
努力是为了不平庸~
在分享的同时加深对于算法的理解,同时吸收他人的奇思妙想,一起见证技术er的成长~
本章将会继续在初入算法(1)——进入算法世界 的基础上继续通过趣学算法进行算法的学习。
一.爆炸增量函数
1.引入故事:《一棋盘的麦子》
有一个古老的传说,一位国王的女儿不幸落水,水中有很多鳄鱼,国王情急之下下令:“谁能把公主救上来,就把女儿嫁给他。”很多人纷纷退让,一个勇敢的小伙子挺身而出,冒着生命危险把公主救了上来,国王一看是个穷小子,想要反悔,说:“除了女儿,你要什么都可以。”小伙子说:“好吧,我只要一棋盘的麦子。您在第1个格子里放1粒麦子,在第2个格子里放2粒,在第3个格子里放4粒,在第4个格子里放8粒,以此类推,每一个格子里麦子的粒数都是前一格子里麦子粒数的两倍。把这64个格子放满了就行,我就要这么多。”国王听后哈哈大笑,觉得小伙子的要求很容易满足,满口答应。结果发现,把全国的麦子都拿来,也填不完这64个格子…..…国王无奈,只好把女儿嫁给了这个小伙子。

解析:通过这个故事,算出64格可放的麦子,总和为S
S=1+2一次方+2的二次方+2的三次方......+2的63次方①
对式①等号的两边乘以2,等式仍然成立
2S=2的一次方+2的二次方+2的三次方+....+2的64次方
用式②减去①得
S=2的64次方-1= 18 446 744 073 709 551615
重量=7729000(亿千克)
我们称这样的函数为爆炸增量函数。
2.算法中的时间复杂度
如果算法的时间复杂度是O(2n次方)
会怎样?随着n的增长,算法会不会“爆掉”?我们经常见到有些算法调试没问题,
运行一段时间也没问题,但在关键的时候宕机(shutdown)。
例如:在线考试系
统,50人考试没问题,100人考试也没问题,但如果全校10000人考试就可能宕机。
科普:宕机就是死机,指计算机无法正常工作,包括一切原因导致的死机。计算机主机出现意外故障而死机,一些服务器(如数据库服务器)死锁,服务器的某些服务停止运行等,都可以称为宕机。
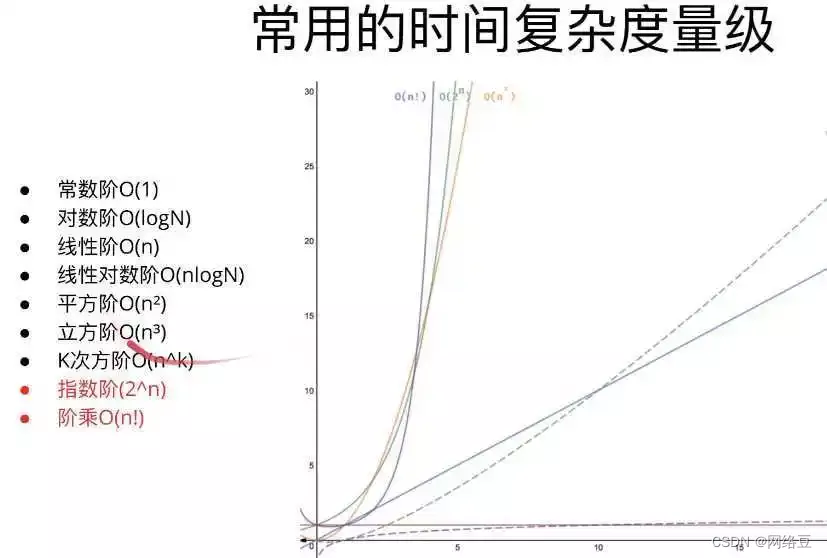
3.常见的时间复杂度类型
(1)常数阶
常数阶算法的运行次数是一个常数,如5、20、100。常数阶算法的时间复杂度通常用O(1)表示。
(2)多项式阶
很多算法的时间复杂度是多项式,通常用O(n)、O(n²)、O(n³)等表示。
(3)指数阶
指数阶算法的运行效率极差,程序员往往像躲“恶魔”一样避开这种算法。指数阶算法的时间复杂度通常用O(2ⁿ)、O(n!)、O(nⁿ)等表示。
(4)对数阶
对数阶算法的运行效率较高,通常用O(logn)、O(nlogn)等表示。
二.兔子数列
1.什么是兔子数列
兔子数列又称斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)在现代物理、准晶体结构、化学等领域,斐波那契数列都有直接的应用,为此,美国数学会从 1963 年起出版了以《斐波那契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果

例子:
假设第1个月有1对初生的兔子,第2个月进入成熟期,第3个月开始生育兔子,而1对成熟的兔子每月会生1对兔子,兔子永不死去…….那么,由1对初生的兔子开始,12个月后会有多少对兔子呢?
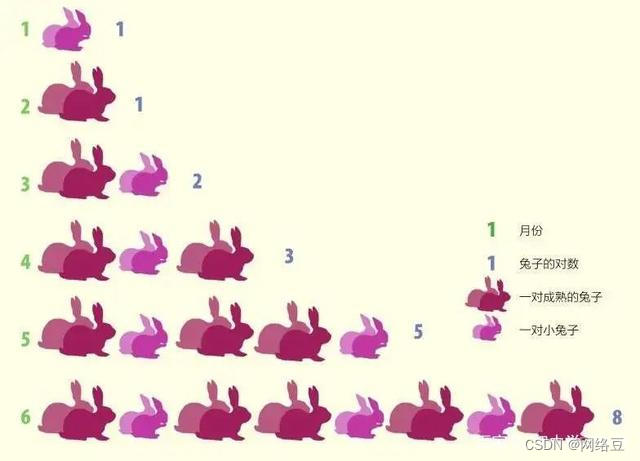
当月兔子数=上月兔子数+上上月兔子数
算法设计:递归算法
int Fib1(int n){
if(n==1||n==2)
return 1;
return Fib1(n-1)+Fib1(n-2);
}算法验证:
假设T(n)表示计算Fib1(n)所需的基本操作次数,那么:
n=1时,T(n)=1;
n=2时,T(n)=1;
n=3时,T(n)=3;//调用Fib1(2)和Fib1(1)并执行一次加法运算(Fib1(2)+Fib1(1))
因此,当n>2时需要分别调用Fib1(n-1)和Fib1(n-2)并执行一次加法运算,换
言之:
n>2时,T(n)=T(n-1)+T(n-2)+1;
递归表达式和时间复杂度T(n)的关系如下:
由此可得:
如何算出F(n)?
求出斐波那契数列的通项公式:

2.递推公式
斐波那契数列:1,1,2,3,5,8,13,21,34,55,89...
如果设an为该数列的第n项(),那么这句话可以写成如下形式:
显然这是一个线性递推数列
通项公式内容
(如上,又称为“比内公式”,是用无理数表示有理数的一个范例。)
3.尾数循环
斐波那契数列的个位数:一个60步的循环
11235,83145,94370,77415,61785,38190,
99875,27965,16730,33695,49325,72910…
进一步,斐波那契数列的最后两位数是一个300步的循环,最后三位数是一个1500步的循环,最后四位数是一个15000步的循环,最后五位数是一个150000步的循环。
本章就将学的这里,后续将会继续更新算法文章
创作不易,求关注,点赞,收藏,谢谢~