当前位置：首页 > news >正文

NLP - 神经网络与反向传播

news 来源：原创 2024/5/9 16:21:52

使用神经网络进行命名实体识别（二值词窗分类）

根据上下文窗口建立词向量
通过一个神经网络层，通过一个逻辑分类器，得到这个概率是属于特定实体词的预测概率。
另一个分类器来比较说明这个词是哪个实体类型（比较概率）

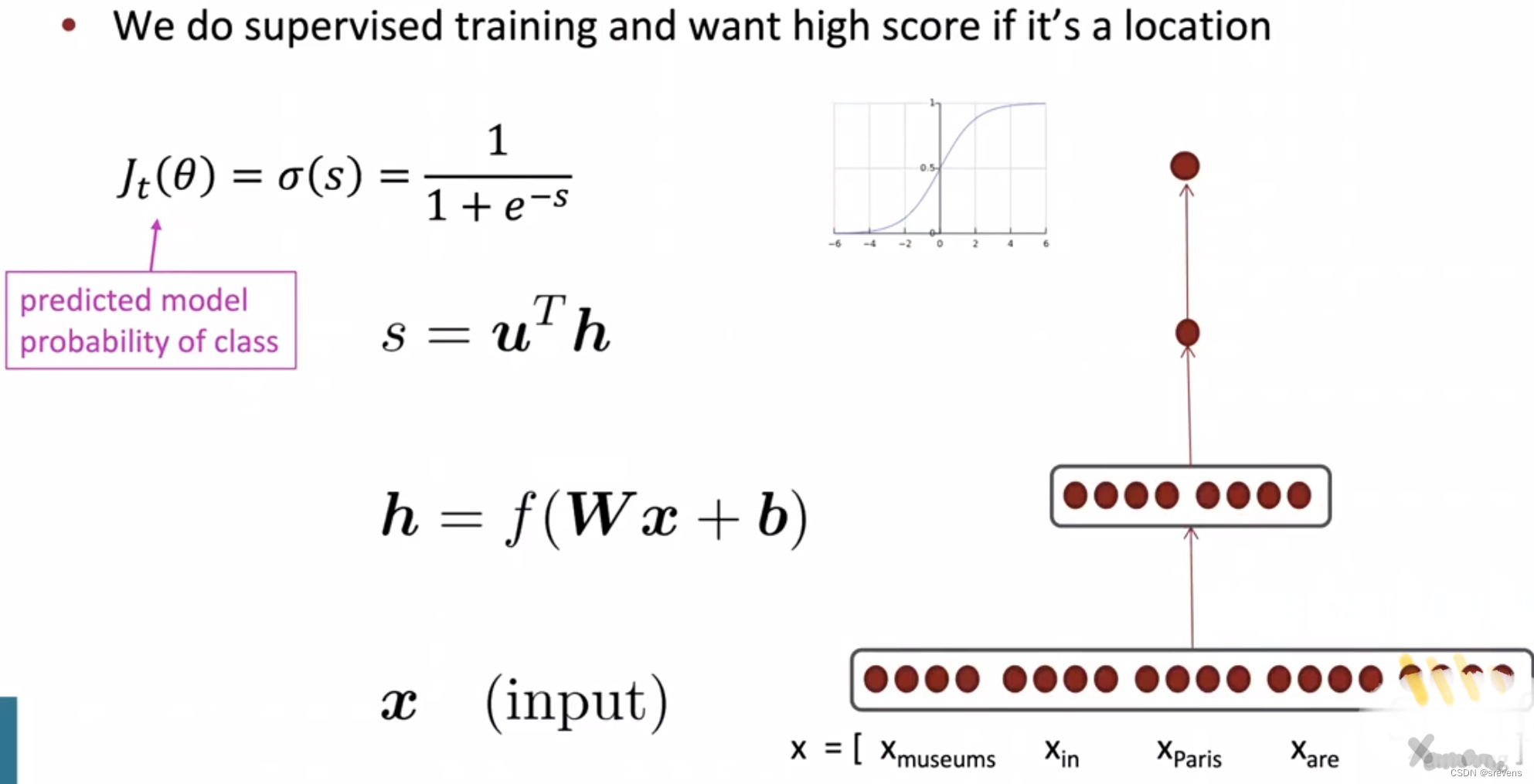
在这里插入图片描述

手工实现梯度下降

基础知识

雅可比矩阵：梯度的推广

给定一个具有 $m$ 输出和 $n$ 输入的函数：
$\boldsymbol{f}(\boldsymbol{x})=[f_1(x_1,x_2,...,x_n),...,f_m(x_1,x_2,...,x_n)]$
它的雅可比矩阵是一个 $m\times n$ 偏导数矩阵：
$\dfrac{\partial\boldsymbol{f}}{\partial\boldsymbol{x}}=\begin{bmatrix}\frac{\partial f_1}{\partial x_1}&\dots&\frac{\partial f_1}{\partial x_n}\\\vdots&\ddots&\vdots\\\frac{\partial f_m}{\partial x_1}&\dots&\frac{\partial f_m}{\partial x_n}\end{bmatrix} \color{red}{\boxed{\left(\frac{\partial f}{\partial x}\right)_{ij}=\frac{\partial f_i}{\partial x_j}}}$

链式法则

对于一变量函数的复合：乘导数
$\begin{aligned} &z=3y \\ &y=x^{2} \\ &\begin{aligned}\frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}=(3)(2x)=6x\end{aligned} \end{aligned}$
对于同时多个变量：乘以雅可比行列式
$\begin{aligned} &\boldsymbol{h}=f(\boldsymbol{z}) \\ &z=\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b} \\ &\begin{aligned}\frac{\partial\boldsymbol{h}}{\partial\boldsymbol{x}}=\frac{\partial\boldsymbol{h}}{\partial\boldsymbol{z}}\frac{\partial\boldsymbol{z}}{\partial\boldsymbol{x}}=...\end{aligned} \end{aligned}$

雅可比行列式示例：逐元素激活函数

$\boldsymbol{h}= f( \boldsymbol{z}) ,\ \, \frac {\partial\boldsymbol{h}}{\partial\boldsymbol{z}}是什么? \ \ \ \ \ \ \ \ h,z\in\mathbb{R}^n$ $h_i=f(z_i)$
$\begin{aligned} \left(\frac{\partial\boldsymbol{h}}{\partial\boldsymbol{z}}\right)_{ij}& =\frac{\partial h_{i}}{\partial z_{j}}=\frac{\partial}{\partial z_{j}}f(z_{i}) \ \ \ \ \ \ 雅可比行列式的定义 \\ &=\begin{cases}f'(z_i)\quad\text{if }i=j\\0\quad \text{if otherwise}\end{cases} \ \ \ \ \ 常规的一个变量的导数 \end{aligned}$
$\left.\frac{\partial\boldsymbol{h}}{\partial\boldsymbol{z}}=\left(\begin{array}{ccc}f'(z_1)&&0\\&\ddots&\\0&&f'(z_n)\end{array}\right.\right)=\operatorname{diag}(\boldsymbol{f'}(\boldsymbol{z}))$

其他雅可比行列式

$\begin{aligned} &\begin{aligned}\frac{\partial}{\partial\boldsymbol{x}}(\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b})=\boldsymbol{W}\end{aligned} \\ &\begin{aligned}\frac{\partial}{\partial\boldsymbol{b}}(\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b})&=\boldsymbol{I}&\text{(单位矩阵)}\end{aligned} \\ &\begin{aligned}\frac{\partial}{\partial\boldsymbol{u}}(\boldsymbol{u}^T\boldsymbol{h})=\boldsymbol{h}^T\end{aligned} \end{aligned}$

回到神经网络

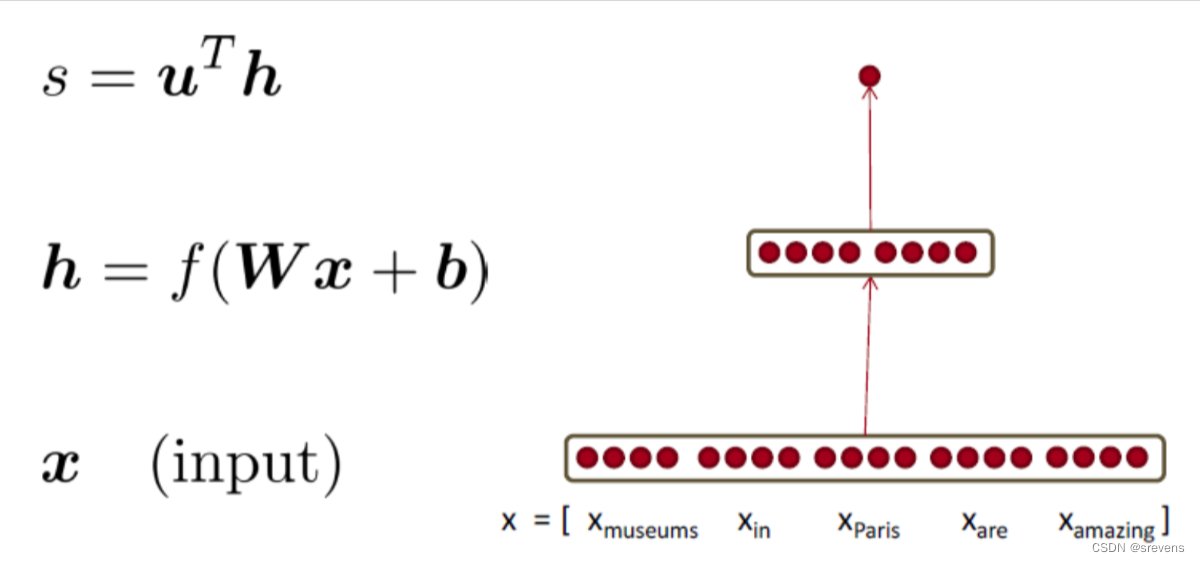
在这里插入图片描述

怎么计算 $\frac{\partial s}{\partial b}$ ？

把等式拆解成简单的几个分块
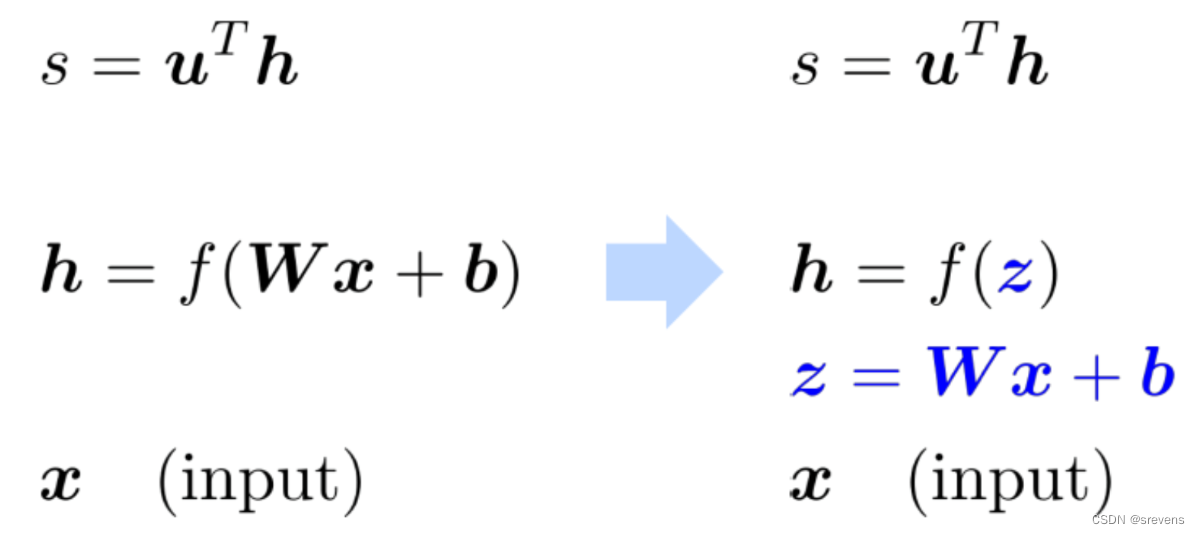
应用链式法则
写下雅各比表达式

怎么计算 $\frac{\partial s}{\partial w}$ ？

在这里插入图片描述
$\delta$ 是局部误差符号，是固定的。

关于矩阵的导数：输出形状

$雅可比公式表达：\\ 如果有一个函数 y = f(x)，其中 x 是一个向量，y 是一个向量，\\ 则雅可比矩阵\ J\ 的元素\ J_{ij}\ 表示\ y_i\ 对\ x_j\ 的偏导数。$

$W\in\mathbb{R}^{n\times m}$ , $\frac{\partial s}{\partial W}$ 的形状是：

“ 给定一个具有 $m$ 输出和 $n$ 输入的函数，它的雅可比矩阵是一个 $m\times n$ 偏导数矩阵。”
1个输出， $n\times m$ 个输入，得到的应该是 $1\times nm$ 的雅可比矩阵？一个很长的低向量
- 问题： 这样不方便更新参数 $\theta^{new}=\theta^{old}-\alpha\nabla_\theta J(\theta)$ ，都应该是 $n\times m$
- 解决： 脱离数学，使用形状约定：导数的矩阵形状等于参数的矩阵形状
  - $\frac{\partial s}{\partial W}$ 的形状是 $n\times m$
  - $\left.\left[\begin{matrix}\frac{\partial s}{\partial W_{11}}&\cdots&\frac{\partial s}{\partial W_{1m}}\\\vdots&\ddots&\vdots\\\frac{\partial s}{\partial W_{n1}}&\cdots&\frac{\partial s}{\partial W_{nm}}\end{matrix}\right.\right]$

$b\in\mathbb{R}^{n\times 1}$ , $\frac{\partial s}{\partial b}$ 的形状是：

$\frac{\partial s}{\partial\boldsymbol{b}}=\boldsymbol{h}^T\circ f^{\prime}(z)$ 是行向量
但是习惯上梯度应该是一个列向量因为 $b$ 是一个列向量

雅可比矩阵形式(这使得链式法则很容易，对计算微积分很有意义) 和形状约定(这使得SGD很容易实现)之间的分歧。

解决：两个选择
- 尽量使用雅可比矩阵形式（不完全使用），最后按照形状约定进行整形
  - 最后转置 $\frac{\partial s}{\partial b}$ 使导数成为列向量（而不是按照雅各比矩阵形式的行向量），
  - 通过 $\delta^T$ 来实现，这样始终遵循形状约定。
- 一直遵循形状约定
  - 查看维度，找出何时转置和/或重新排序项。

关于矩阵的导数（按照雅各比矩阵形式）

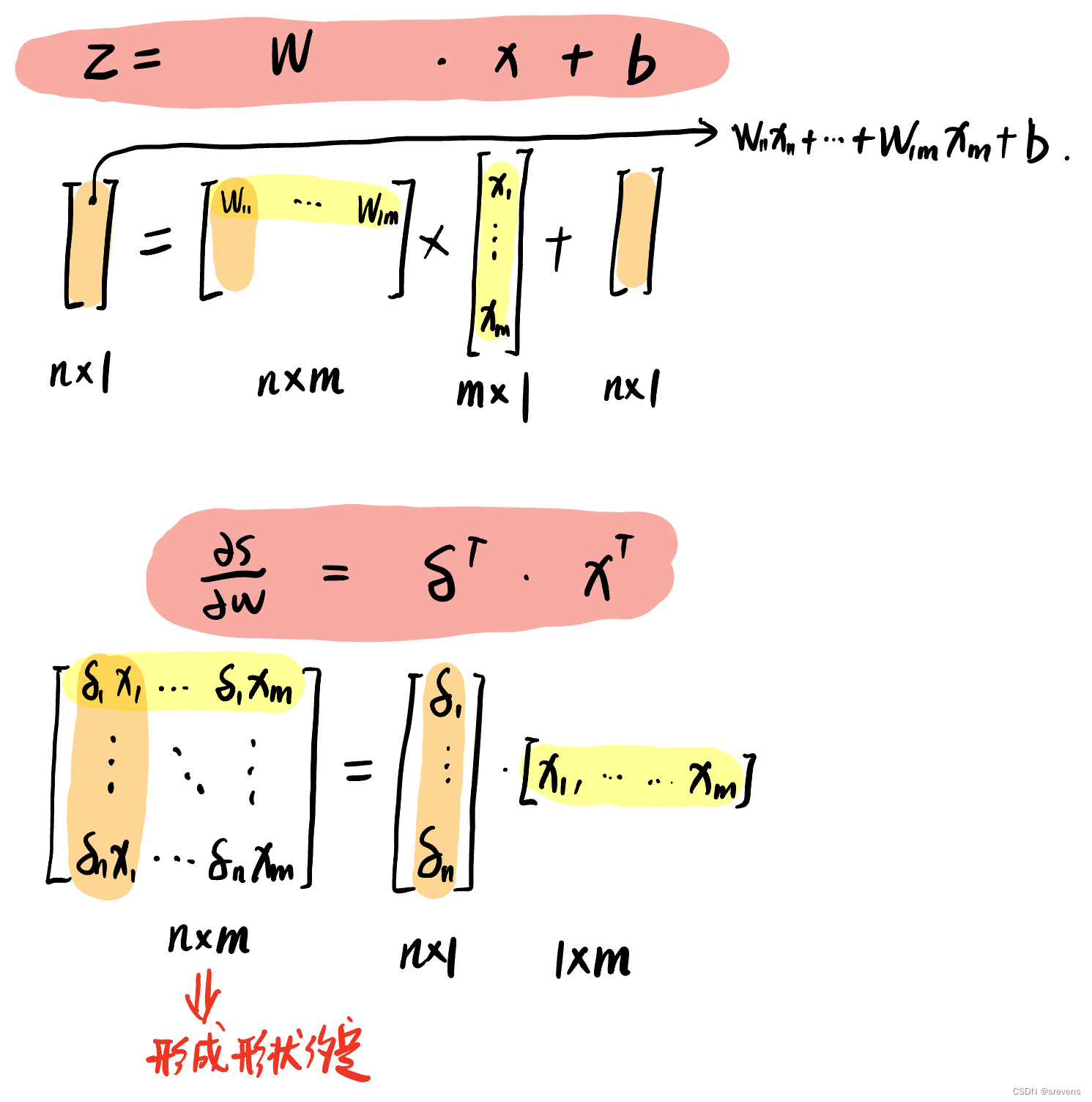
$\quad\frac{\partial s}{\partial W}=\boldsymbol{\delta}\frac{\partial z}{\partial W}$

$\delta$ 将出现在我们的答案中。
另一项应该是 $x$ ,因为 $z = W x + b$

$\quad\frac{\partial s}{\partial b}=\boldsymbol{\delta}\frac{\partial z}{\partial b}$

$\delta$ 将出现在我们的答案中。
另一项应该是 $1$ ,因为 $z = W x + b$

这表明 $\frac{\partial s}{\partial W}=\boldsymbol{\delta}^T\boldsymbol{x}^T$ $\frac{\partial s}{\partial b}=\boldsymbol{\delta}^T$

$\delta$ 是 z 处的局部误差信号
x 是本地输入信号

总结

在这里插入图片描述

反向传播

求导，使用链式法则

构建计算图

前向传播阶段

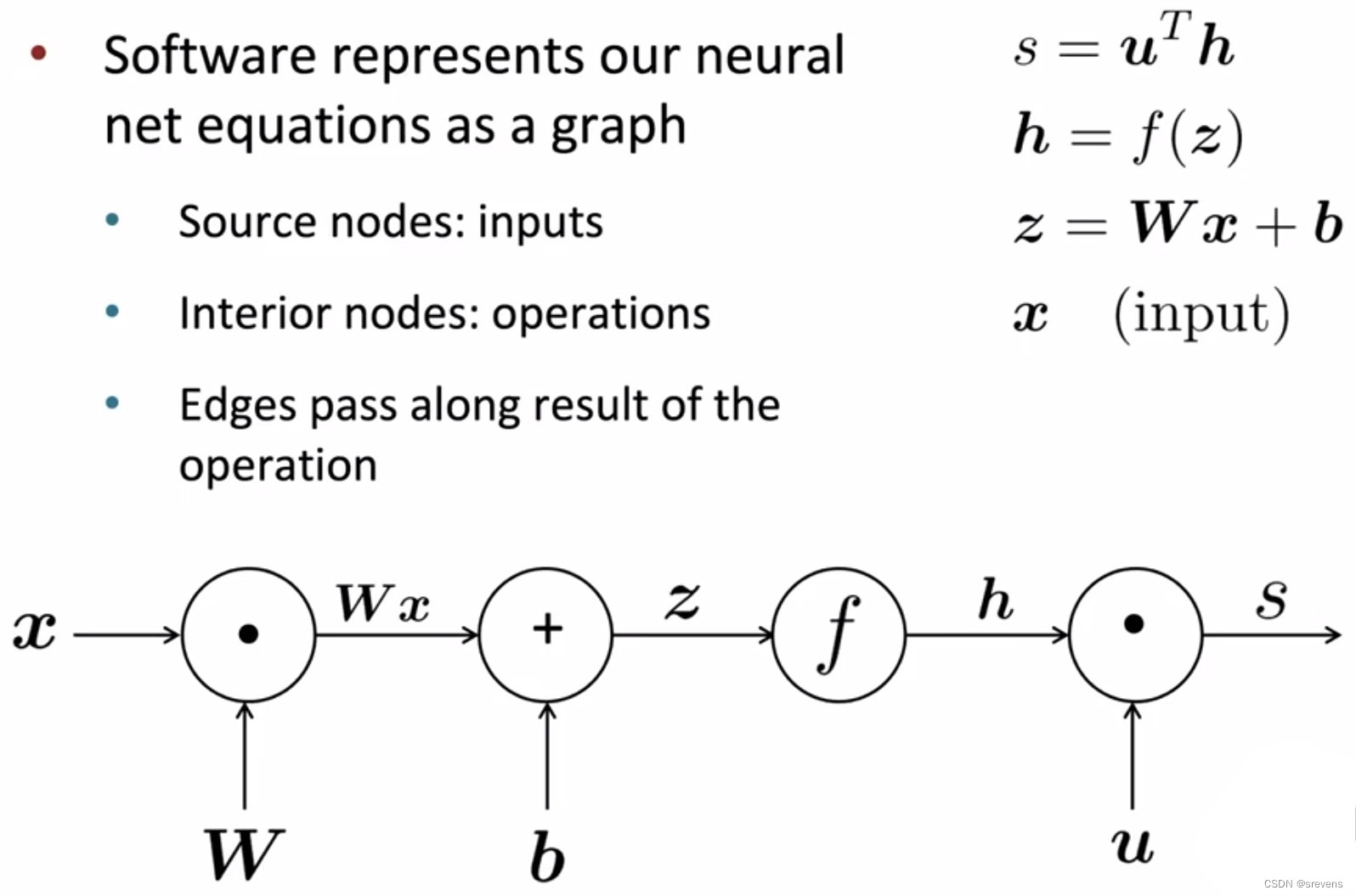
神经网络的基本附加元素是 发回梯度，告诉我们怎么更新模型的参数，使得模型在获得损失函数后进行学习（最小化损失）。

反向传播阶段
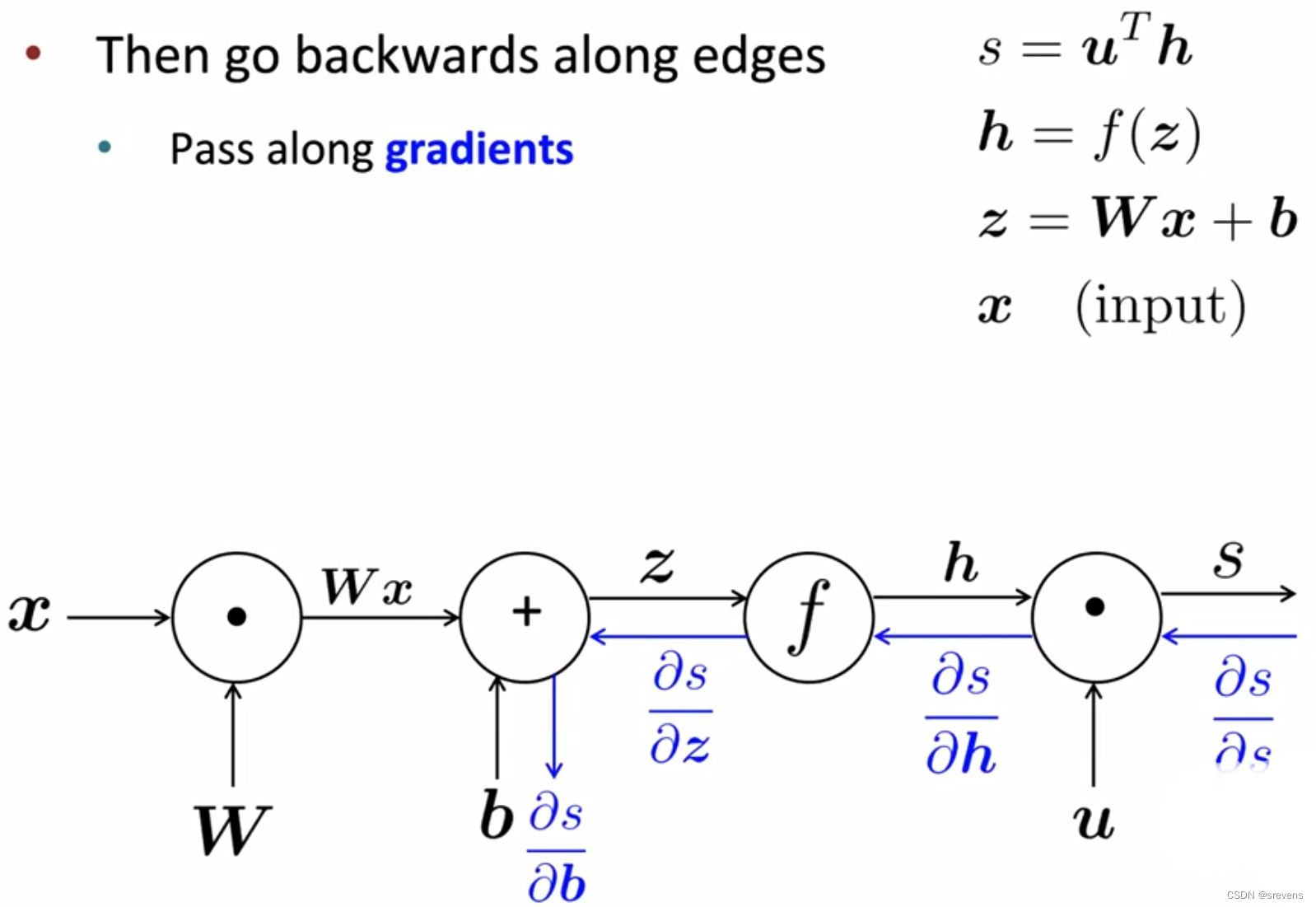
反向传播：单个节点
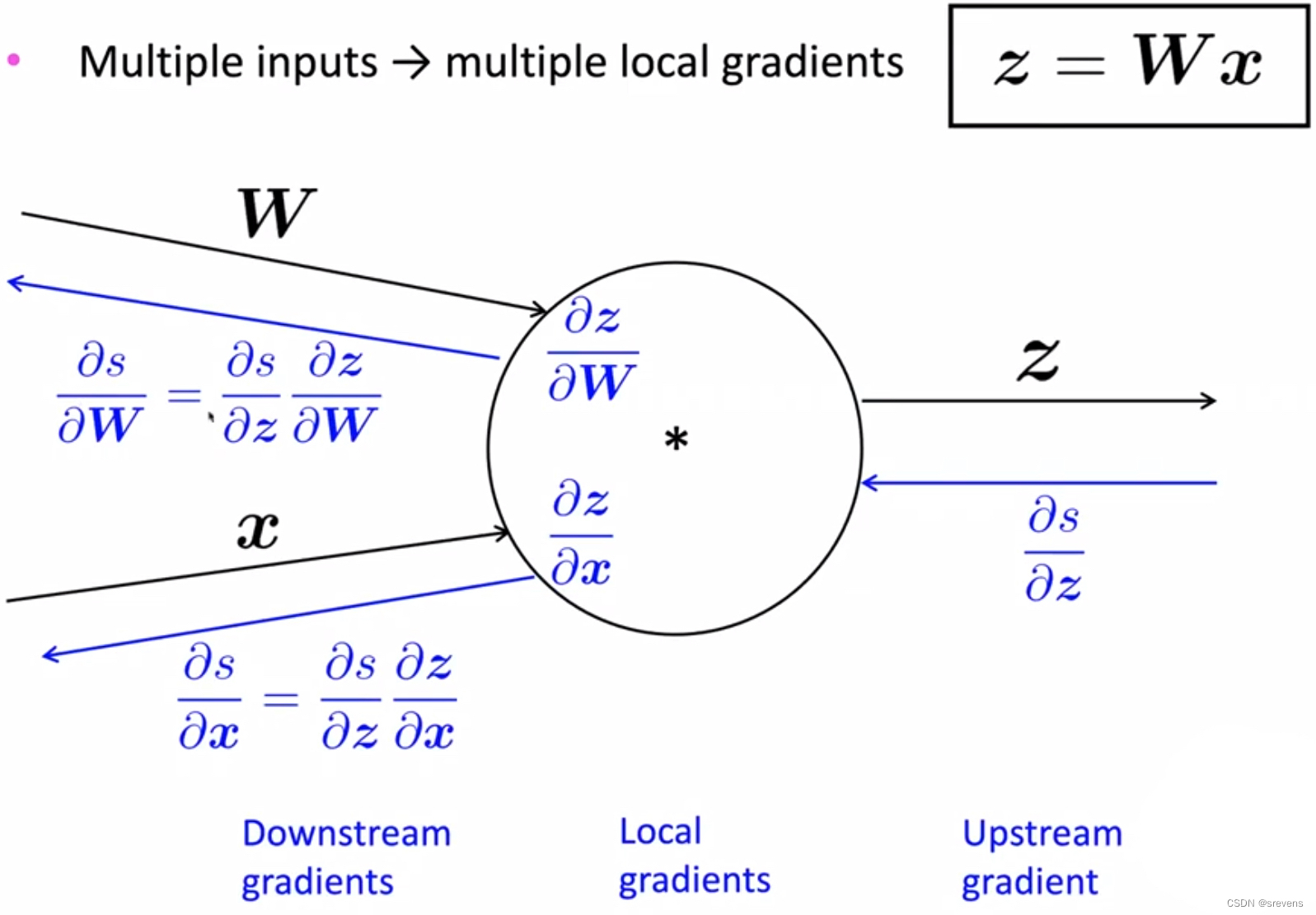
反向传播：多个节点
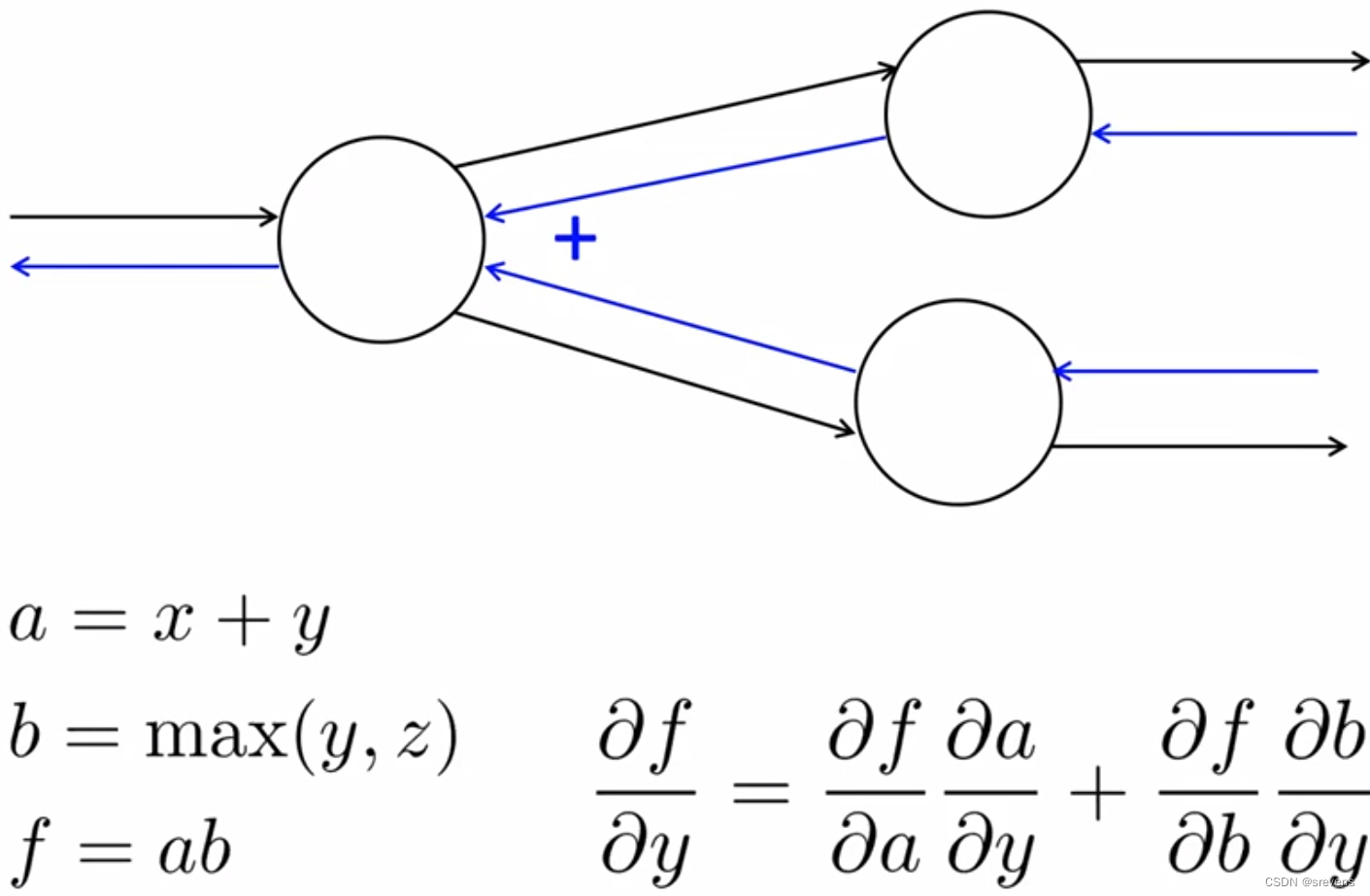
一个例子
反向传播最后的结果体现 改变输入对输出的影响，上涨/减少这个变量的多少倍

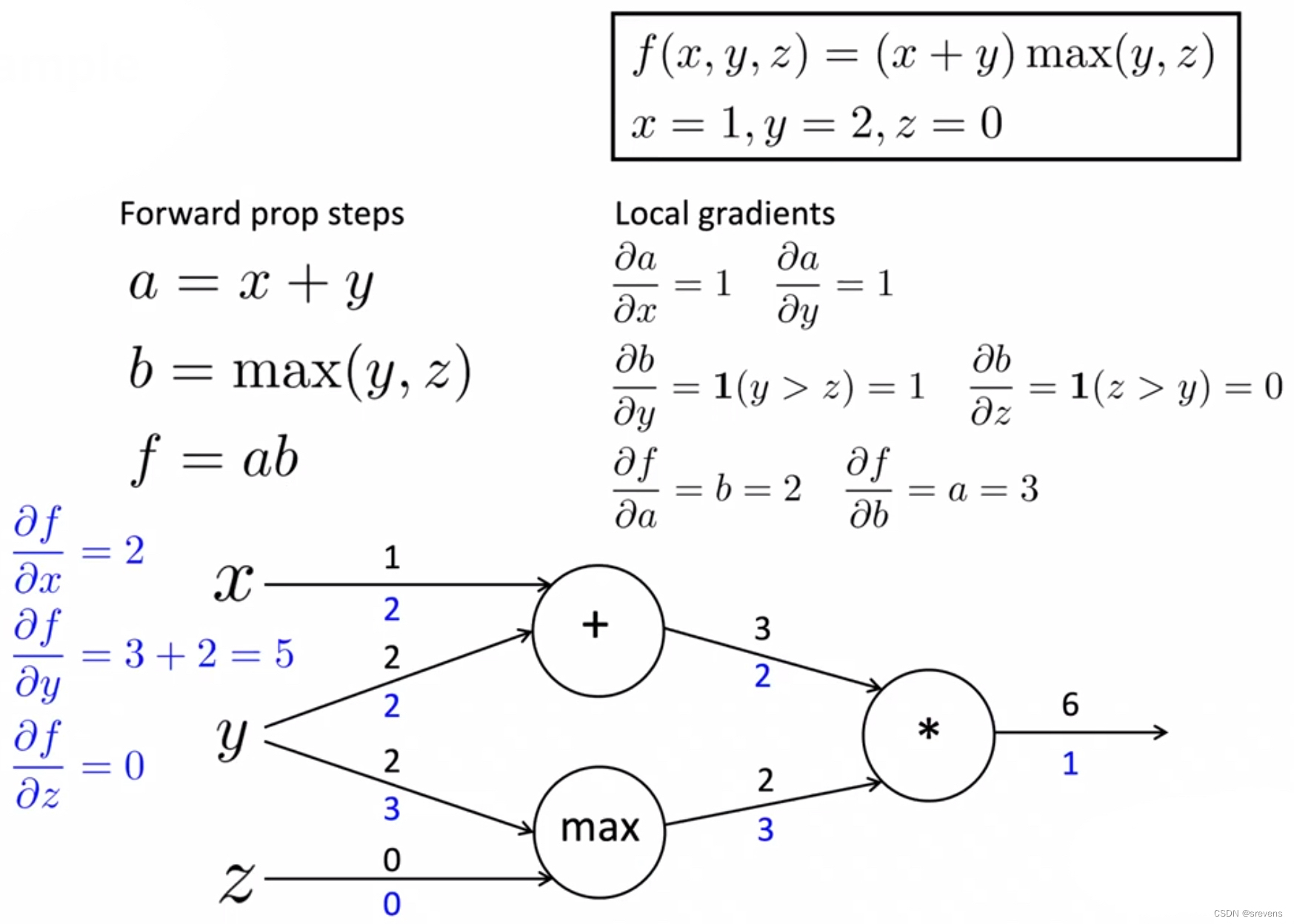
开始计算

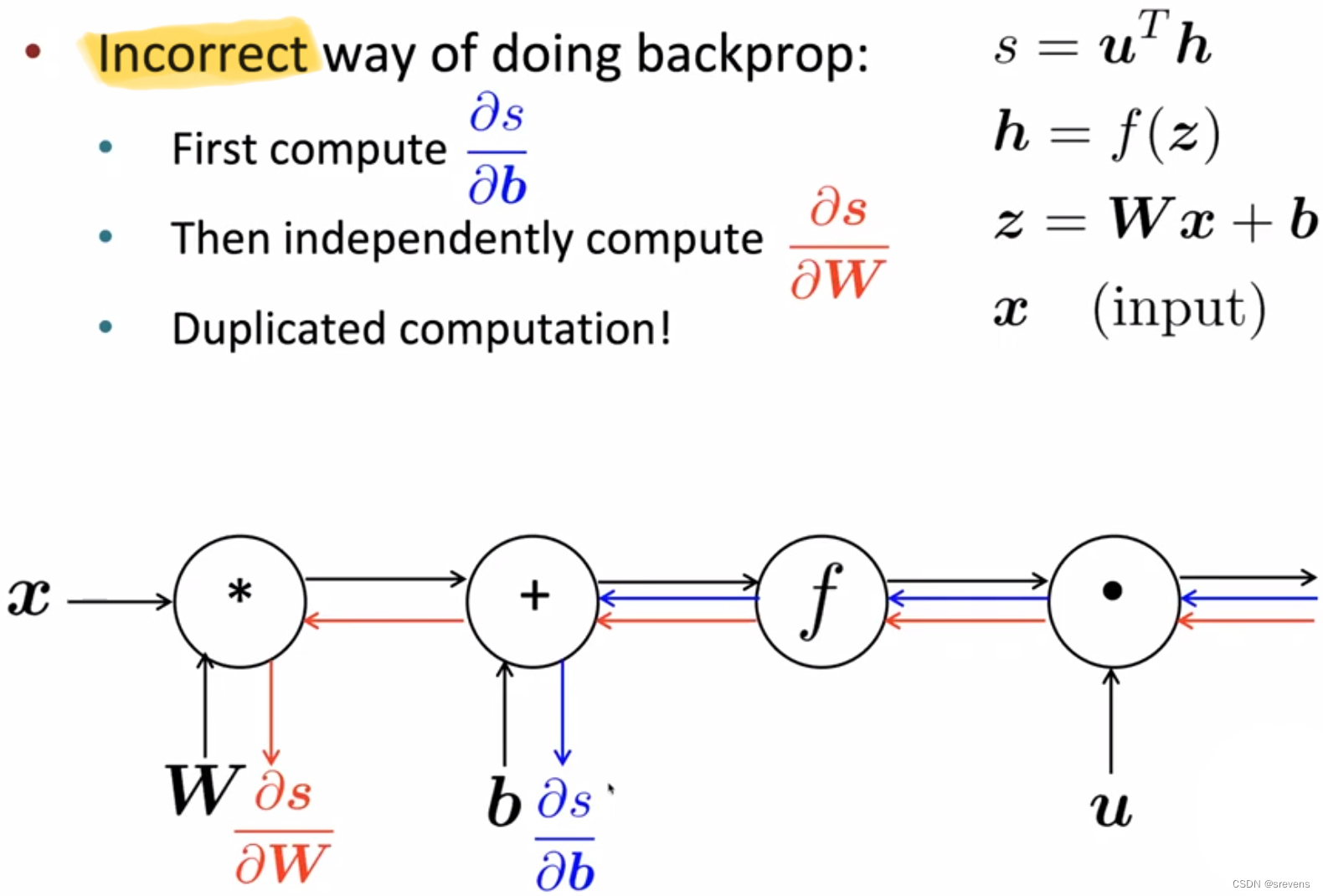
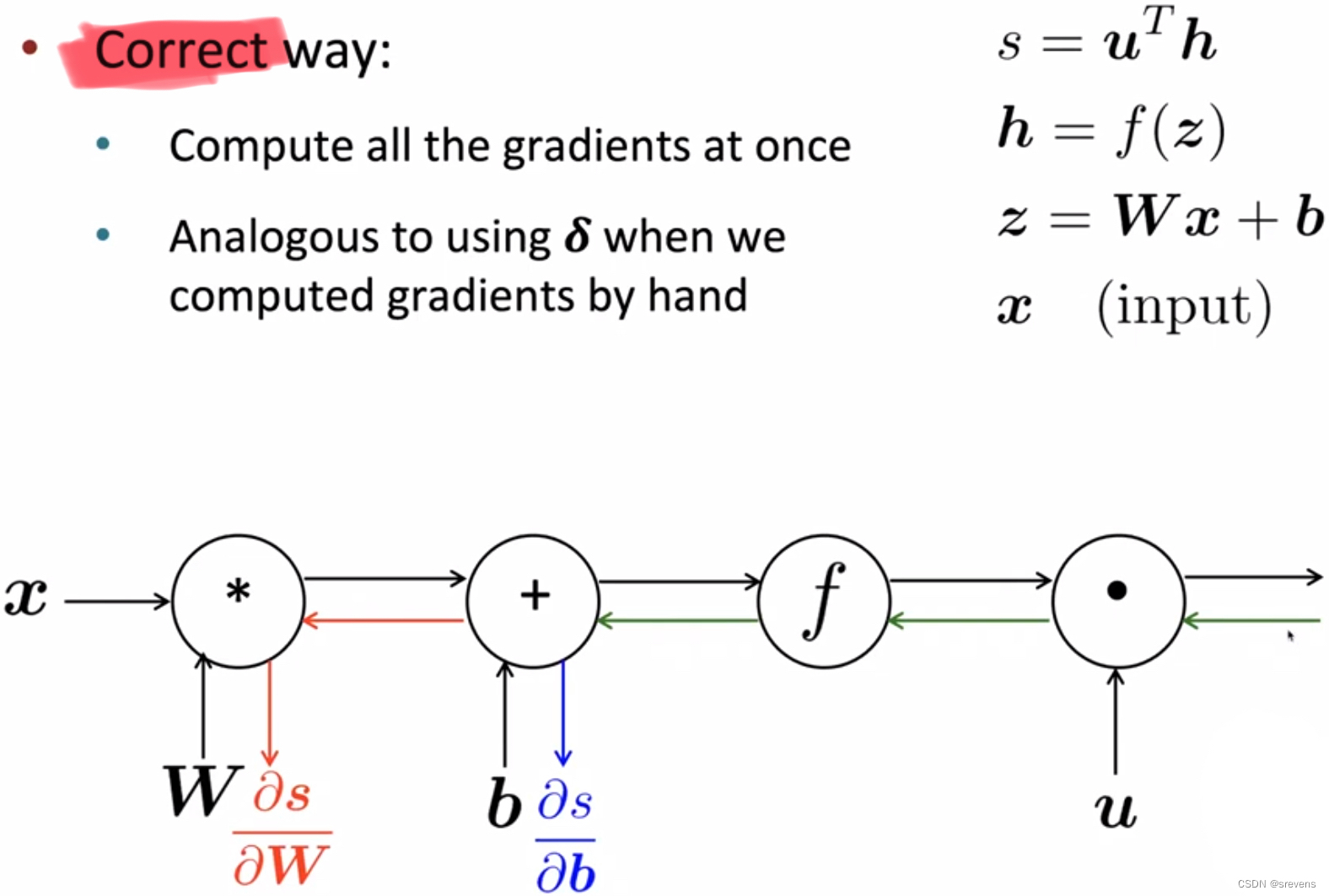
在这里插入图片描述

就像前面手动计算梯度下降那样

在一般的计算图中进行反向传播计算的流程

在这里插入图片描述

现在的深度学习神经网络框架(Tensorflow, PyTorch, etc…)可以自动做反向传播，但是主要让层/节点编写器手动计算局部导数。我们需要为图中的特定节点或层添加内容。

反向传播的具体实现

class ComputationalGraph(object):#..... def forward(inputs):# 1.[pass inputs to input gates...] # 2. forward the computational graph: # 根据节点在计算图中的依赖关系对节点进行拓扑排序for gate in self .graph.nodes_topologically_sorted(): gate.forward()return loss # the final gate in the graph outputs the loss def backward():# 反转图的拓扑排序for gate in reversed(self.graph.nodes_topologically_sorted()):gate.backward() # little piece of backprop (chain rule applied) return inputs_gradients

手动实现前向/后向API

在这里插入图片描述

总结

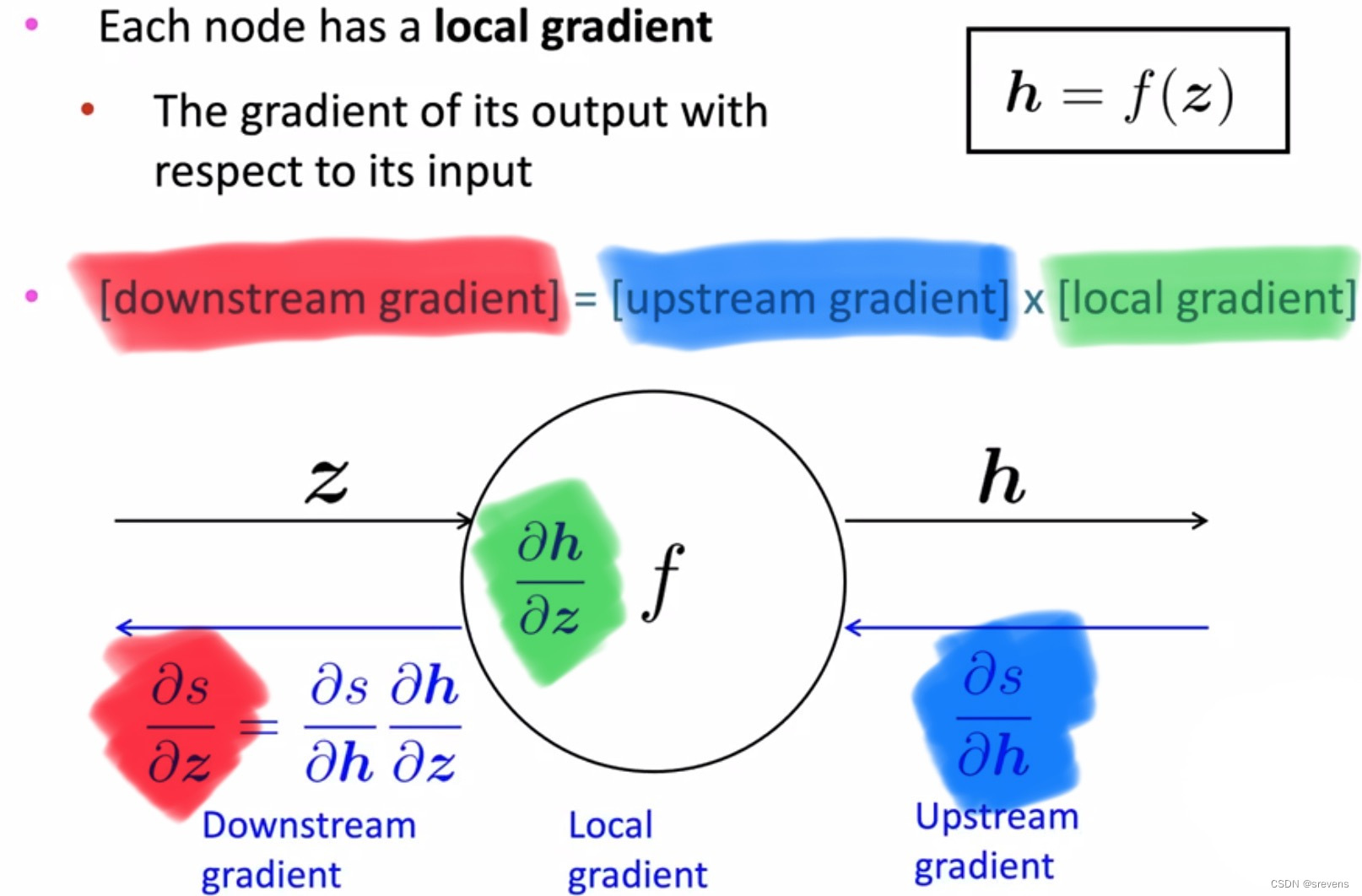
反向传播：下游梯度 = 上游梯度 * 局部梯度
前向传播计算出当前参数的值，然后进行反向传播以计算出损失的梯度（当前参数的损失）。
现在的深度学习神经网络框架(Tensorflow, PyTorch, etc…)可以自动做反向传播，我们不用知道具体是怎么操作的，就像我们使用gcc来编译c代码，但是我们不需要具体知道gcc是怎么操作的。