EM@解三角形@正弦定理@余弦定理
文章目录
- abstract
- 解三角形
- 基本原理
- 不唯一性
- 正弦定理
- 直角三角形中的情形
- 推广
- 锐角三角形
- 钝角情形
- 小结:正弦定理
- 余弦定理
- 直角三角形中的情形
- 非直角情形
- 小结:余弦定理
- 公式的角余弦形式
abstract
- 解直角三角形问题
- 正弦定理和余弦定理的推导
- 对于非直角情形,都是直角情形的推广
- 同过构造辅助线(垂线),来构造直角三角形,利用直角三角形的特点构建恒等方程,得到相应的定理
解三角形
- 一般地,我们把三角形的3个角和它的对边分别叫做三角形的元素,已知三角形的某几个元素求其余元素的过程称为解三角形
基本原理
- 三角形内角和为 π \pi π
- 正弦定理
- 余弦定理
不唯一性
- 某些条件下可以给出不只一个的解
- 当已知条件是全等三角形的条时,具有唯一解,否则可能有2个解
- 例如,已知 A , B A,B A,B, a a a,具有唯一解
- 而已知 a , b , A a,b,A a,b,A,则可能具有2个解
正弦定理
- 正弦定理揭示了:在任意一个三角形中,角与它对应的边之间在数量上的关系
- 设三角形 A B C ABC ABC中, A , B , C A,B,C A,B,C的对边分别为 a , b , c a,b,c a,b,c;角 ∠ A \angle{A} ∠A可以简写为 A A A, ∠ B , ∠ C \angle{B},\angle{C} ∠B,∠C类似得可以简写为 B , C B,C B,C
直角三角形中的情形
- 当 ∠ C = π 2 \angle{C}=\frac{\pi}{2} ∠C=2π时:
- 显然 a c = sin A \frac{a}{c}=\sin{A} ca=sinA, b c = sin B \frac{b}{c}={\sin{B}} cb=sinB,即有 a sin A \frac{a}{\sin{A}} sinAa= b sin B \frac{b}{\sin{B}} sinBb= c c c
(1)- 且 sin C = sin π 2 \sin{C}=\sin{\frac{\pi}{2}} sinC=sin2π= 1 1 1,从而 c c c= c 1 \frac{c}{1} 1c= c sin C \frac{c}{\sin{C}} sinCc
- 因此式(1)改写为 a sin A \frac{a}{\sin{A}} sinAa= b sin B \frac{b}{\sin{B}} sinBb= c sin C \frac{c}{\sin{C}} sinCc
(2)
- 显然 a c = sin A \frac{a}{c}=\sin{A} ca=sinA, b c = sin B \frac{b}{c}={\sin{B}} cb=sinB,即有 a sin A \frac{a}{\sin{A}} sinAa= b sin B \frac{b}{\sin{B}} sinBb= c c c
推广
- 在一般三角形中,式(2)仍然成立
锐角三角形
- 当 A , B , C A,B,C A,B,C对应的角都时锐角时
- 过点 C C C作 C D ⊥ A B CD\perp{AB} CD⊥AB于点 D D D
- 显然 C D b \frac{CD}{b} bCD= sin A \sin{A} sinA; C D a sin B \frac{CD}{a}\sin{B} aCDsinB,分别变形,可得
- C D = b sin A CD=b\sin{A} CD=bsinA
- C D = a sin B CD=a\sin{B} CD=asinB
- 即 b sin A b\sin{A} bsinA= a sin B a\sin{B} asinB,变形(两边同时除以 sin A sin B \sin{A}\sin{B} sinAsinB,得 a sin A \frac{a}{\sin{A}} sinAa= b sin B \frac{b}{\sin{B}} sinBb
(3)
- 显然 C D b \frac{CD}{b} bCD= sin A \sin{A} sinA; C D a sin B \frac{CD}{a}\sin{B} aCDsinB,分别变形,可得
- 同理,过点 B B B作辅助线同样可证 a sin A \frac{a}{\sin{A}} sinAa= c sin C \frac{c}{\sin{C}} sinCc
(4),若过点 A A A作辅助线可得 b sin B \frac{b}{\sin{B}} sinBb= c sin C \frac{c}{\sin{C}} sinCc(5) - 由式(3,4)可知(2)成立
- 过点 C C C作 C D ⊥ A B CD\perp{AB} CD⊥AB于点 D D D
钝角情形
- 不妨设 ∠ B > π 2 \angle{B}>\frac{\pi}{2} ∠B>2π,作 C D ⊥ A B CD\perp{AB} CD⊥AB,交 A B AB AB的延长线于点 D D D
- 则 C D b \frac{CD}{b} bCD= sin A \sin{A} sinA; C D a = sin ( π − B ) \frac{CD}{a}=\sin{(\pi-{B})} aCD=sin(π−B)= sin B \sin{B} sinB
- 从而有 C D CD CD= b sin B b\sin{B} bsinB= a sin B a\sin{B} asinB
(6),变形可得式(3) - 同理(比如过点 A A A作辅助线),可得式(5)
- 所以式(2)此情形也成立
小结:正弦定理
- 在任意一个三角行中,各边的长和它所对的角的正弦的比相等,即 a sin A \frac{a}{\sin{A}} sinAa= b sin B \frac{b}{\sin{B}} sinBb= c sin C \frac{c}{\sin{C}} sinCc
- 解三角形问题中,若已知条件有角及其对边,那么可以考虑使用正弦定理,例如 a , b , A a,b,A a,b,A
余弦定理
-
若已知一个三角形的两边即其夹角,则该三角形唯一地完全确定
- 这类情况无法直接应用正弦定理,因为已知条件中的角是夹角而不是已知边的对角
-
为了解这类三角形,需要新的途径,也就是余弦定理
-
设三角形 A B C ABC ABC中已知 ∠ C \angle{C} ∠C,且其邻边 a , b a,b a,b已知
直角三角形中的情形
- 若 ∠ C \angle{C} ∠C= π 2 \frac{\pi}{2} 2π,则可以用勾股定理求出 c c c
非直角情形
-
情形1 情形2 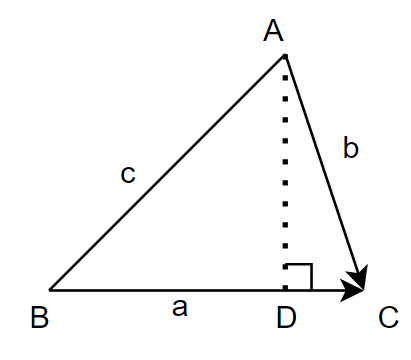
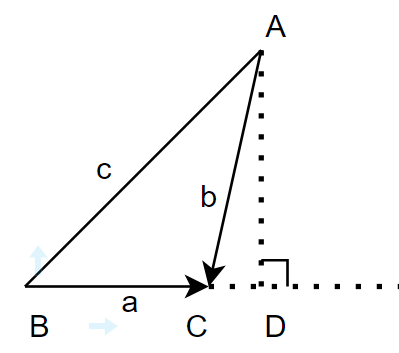
∠ C < π 2 \angle{C}<\frac{\pi}{2} ∠C<2π ∠ C > π 2 \angle{C}>\frac{\pi}{2} ∠C>2π -
当 ∠ C < π 2 \angle{C}<\frac{\pi}{2} ∠C<2π时: B D BD BD= a − b cos C a-b\cos{C} a−bcosC
(1); A D AD AD= b sin C b\sin{C} bsinC(2) -
当 ∠ C > π 2 \angle{C}>\frac{\pi}{2} ∠C>2π时; B D BD BD= a + b cos ( π − C ) a+b\cos{(\pi-C)} a+bcos(π−C)= a − b cos C a-b\cos{C} a−bcosC; A D AD AD= b sin ( π − C ) b\sin{(\pi-C)} bsin(π−C)= b sin C b\sin{C} bsinC
-
容易看出,无论 ∠ C \angle{C} ∠C是锐角还是钝角,都有
- B D BD BD= a − b cos C a-b\cos{C} a−bcosC
- A D AD AD= b sin C b\sin{C} bsinC
-
在情形1和2中都有直角三角形 A D B ADB ADB, ∠ D = π 2 \angle{D}=\frac{\pi}{2} ∠D=2π
- 应用勾股定理, c 2 c^2 c2= A D 2 + B D 2 AD^2+BD^2 AD2+BD2
(3) - 代入(1,2),得 c 2 = b 2 sin 2 C + ( a − b cos C ) 2 c^2=b^2\sin^2{C}+(a-b\cos{C})^2 c2=b2sin2C+(a−bcosC)2= a 2 + b 2 − 2 a b cos C a^2+b^2-2ab\cos{C} a2+b2−2abcosC
(4-1)
- 应用勾股定理, c 2 c^2 c2= A D 2 + B D 2 AD^2+BD^2 AD2+BD2
-
同理, a 2 a^2 a2= a 2 + c 2 − 2 a c cos B a^2+c^2-2ac\cos{B} a2+c2−2accosB
(4-2); c 2 c^2 c2= a 2 + b 2 − 2 b c cos A a^2+b^2-2bc\cos{A} a2+b2−2bccosA(4-3)
小结:余弦定理
- 三角形任何一边的平方等于其他两边的平方和减去两边与它们夹角的余弦的积的2倍即上述公式组(4-1,4-2,4-3)
- 该公式组表述了任意一个三角形中三边长与三个内角余弦之间的数量关系
- 在一个三角形中,若已知两边及其夹角,就可以利用余弦定理求出第三边(唯一)
公式的角余弦形式
- cos A = b 2 + c 2 − a 2 2 b c \cos{A}=\frac{b^2+c^2-a^2}{2bc} cosA=2bcb2+c2−a2
- cos B = a 2 + c 2 − b 2 2 a c \cos{B}=\frac{a^2+c^2-b^2}{2ac} cosB=2aca2+c2−b2
- cos C = a 2 + b 2 − c 2 2 a b \cos{C}=\frac{a^2+b^2-c^2}{2ab} cosC=2aba2+b2−c2
