一种基于约化因子上三角矩阵求逆方法与MATLAB仿真
一种基于约化因子上三角矩阵求逆的方法与MATLAB仿真
目录
前言
一、上三角矩阵单位化
二、C对角矩阵求逆
三、A' 矩阵求逆
四、A矩阵求逆
五、计算量分析
六、MATLAB仿真
七、参考资料
总结
前言
矩阵运算广泛应用于实时性要求的各类电路中,其中矩阵求逆运算最难以实现。本文是在阅读文献后,仿真文中采用的一种约化因子求逆的优化算法,将任意一个 n×n 阶 上三角矩阵转换成对角线为 1 的上三角矩阵,使得除法运算与乘加运算分离开来,大大简化矩阵求逆运算过程。文献中有些地方表述有误,在撰写本文时已经改正。
提示:以下是本篇文章正文内容,希望能帮助到各位,转载请附上链接。
一、上三角矩阵单位化
假设A为N×N阶上三角矩阵,其对角线元素非0,可以通过变换将其用一个对角矩阵C和对角线为1的上三角矩阵A'的乘积表示。
其中
通式为
二、C对角矩阵求逆
对于C这个对角矩阵求逆很简单,只需要对其对角元取倒数即可。
三、A' 矩阵求逆
对于上三角矩阵A',每个 2 行 2 列交集所构成的二阶子矩阵,称为操作矩阵,如
构成一个操作矩阵,每次进行行变换的效果体现在操作矩阵的右上角元素上,即令,则
称为约化因子,其通式为
则可求出A' 的逆矩阵,即为
需要计算(N-1)(N-2)/2个元素。
根据公式,计算时,会发现需要先求
,其他都已知,会发现他俩的下标n一样,区别在于表示行的下标,而且k>m,所以计算时每一列从下至上依次计算,列与列之间互不影响。
谈到这里,是不是会发现如果在FPGA上面用此方法计算上三角矩阵的逆矩阵会大大提高速度,因为关键的计算就在于A' 的逆矩阵的计算,而计算其逆矩阵时列与列又互不影响,直接可以并行计算。
四、A矩阵求逆
由于,那么
由于是个对角阵,所以也可以表示为
。
五、计算量分析
限制,否则根据前面的分析根本不需要求
。
对N×N阶对角矩阵C求逆需要N次除法。
将一个主对角元素非0且非1的N×N阶矩阵A变为一个主对角元素全1的矩阵A'和对角矩阵C需要运算的乘法次数(将除法看成去乘以C逆矩阵的对角元)为:
求的第n(n≥3)列需要的乘法次数与加法(在FPGA中实现时,减法可以看成加法)次数相等,均为
那么计算所有的列需要的乘法与加法次数均为:
其中用到公式
最后计算需要的乘法次数为
因为是对角元为1的上三角矩阵,
是对角矩阵,所以只有上述表达式的乘法次数。
那么总的运算量为:
乘法:
加法:
除法:
特殊的,如果待求矩阵A本来就是一个主对角线全为1的上三角矩阵,那么就可以省略上三角矩阵单位化,那么阵个求逆只会用到乘法和加法各次。
六、MATLAB仿真
以MATLAB自带求逆函数inv为对比,仿真得出以下结果:
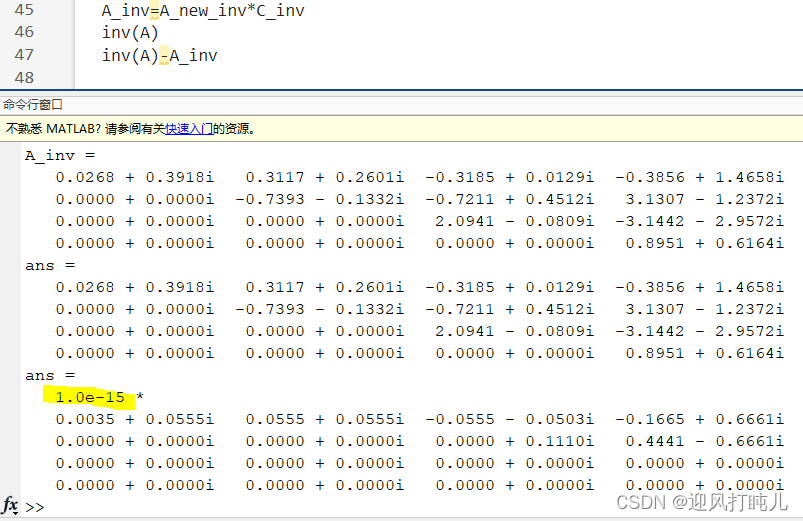
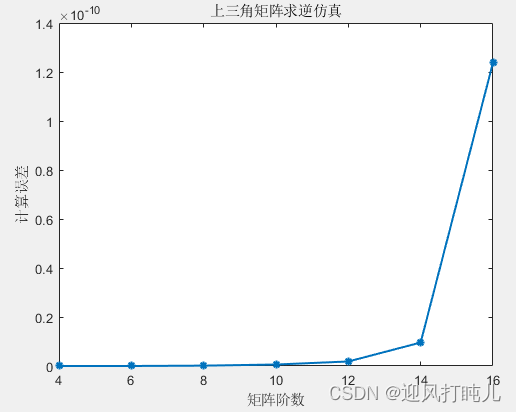

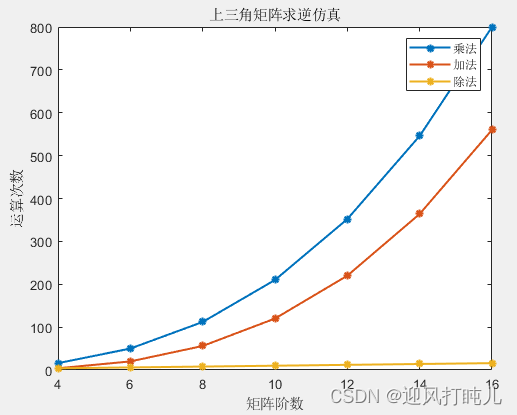
误差定义及源代码见参考资料。
七、参考资料
https://download.csdn.net/download/m0_66360845/89011663
总结
以上介绍了一种基于约化因子上三角矩阵求逆的方法与MATLAB仿真,小伙伴们认真看完必定有收获。
